题目内容
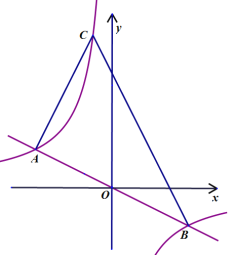
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点
轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ,
,![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() .则点
.则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.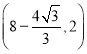 C.
C.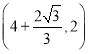 D.
D.![]()
【答案】C
【解析】
延长BC交y轴于点D可求OD,CD的长,进一步求出BD的长,再解直角三角形BPE,求得BP的长,从而可确定点P的坐标.
延长BC交y轴于点D,MN与AB将于点E,如图,

∵四边形OABC是菱形,∠AOC=30°,
∴OA=OC=AB=BC=4,BC∥OA,∠ABC=30°,
∴∠OCD=∠AOC=30°,
∴OD=![]() OC=2,即点P的纵坐标是2.
OC=2,即点P的纵坐标是2.
∴DC=2![]() ,
,
∴BD=BC+CD=4+2![]() ,
,
∵MN是AB的垂直平分线,
∴BE=![]() AB=2,
AB=2,
∴BP= ,
,
∴DP=BD-BP=4+2![]() -
-![]() =4+
=4+![]() .
.
∴点P的坐标为
故选C.

练习册系列答案
相关题目