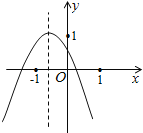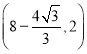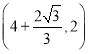题目内容
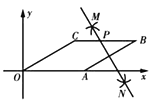
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]()
![]() 的图象相交于点
的图象相交于点![]() 和
和![]() .
.

(1)求一次函数和反比例函数的解析式;
(2)若定义横、纵坐标均为整数的点叫做好点,则图中阴影部分区域内(不含边界)好点的个数为________;
(3)请根据图象直接写出不等式![]() 的解集.
的解集.
【答案】(1)反比例函数的解析式为![]() ,一次函数的解析式为
,一次函数的解析式为![]() ;(2)7个;(3)
;(2)7个;(3)![]() 或
或![]() .
.
【解析】
(1)把A(2,3)代入![]() 可求得k=6,把B(m,-1)代入
可求得k=6,把B(m,-1)代入![]() 得m=-6,把A(2,3),B(-6,-1)代入y=ax+b即可求出a,b的值;
得m=-6,把A(2,3),B(-6,-1)代入y=ax+b即可求出a,b的值;
(2)求出直线![]() 与y轴的交点坐标结合直线与双曲线在第一象限内的交点坐标即可确定好点的个数;
与y轴的交点坐标结合直线与双曲线在第一象限内的交点坐标即可确定好点的个数;
(3)根据图象确定直线在双曲线下方时,确定x的取值范围即可.
(1)将点![]() 代入
代入![]() 得,
得,![]() ,
,
∴反比例函数的解析式为:![]() .
.
将点![]() 代入
代入![]() 得,
得,![]() .
.
将点![]() ,
,![]() 代入
代入![]() 得,
得,
![]()
解得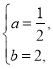
∴一次函数的解析式为:![]() .
.
(2)令x=0,得y=2,所以直线![]() 与y轴的交点坐标为(0,2)
与y轴的交点坐标为(0,2)
故阴影部分内(不含边界)整点坐标有(1,1),(1,2),(1,3),(2,1),(2,2),(4,1),(5,1)共7个;
(3)∵A(2,3),B(-6,1)且![]()
由图象可得x的取值范围是:![]() 或
或![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目