题目内容
 如图,M(0,-4),N(0,-10),过M、N点⊙P的半径为5,反比例函数y=
如图,M(0,-4),N(0,-10),过M、N点⊙P的半径为5,反比例函数y=| k |
| x |
考点:垂径定理,反比例函数图象上点的坐标特征,勾股定理
专题:计算题
分析:作PH⊥MN于H,连结PN,先利用M、N点坐标计算出MN=6,OM=4,再根据垂径定理得到MH=NH=3,然后根据勾股定理计算出PH=4,从而确定P点坐标为(-4,-7),再把P点坐标代入反比例函数解析式中即可得到k的值.
解答: 解:作PH⊥MN于H,连结PN,如图,
解:作PH⊥MN于H,连结PN,如图,
∵M(0,-4),N(0,-10),
∴MN=6,OM=4,
∵PH⊥MN,
∴MH=NH=
MN=3,
∴OH=4+3=7,
在Rt△PHN中,PN=5,NH=3,
∴PH=
=4,
∴P点坐标为(-4,-7),
把P(-4,-7)代入y=
得k=-4×(-7)=28.
故答案为28.
 解:作PH⊥MN于H,连结PN,如图,
解:作PH⊥MN于H,连结PN,如图,∵M(0,-4),N(0,-10),
∴MN=6,OM=4,
∵PH⊥MN,
∴MH=NH=
| 1 |
| 2 |
∴OH=4+3=7,
在Rt△PHN中,PN=5,NH=3,
∴PH=
| PN2-HN2 |
∴P点坐标为(-4,-7),
把P(-4,-7)代入y=
| k |
| x |
故答案为28.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和反比例函数图象上点的坐标特征.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
在1,-2,
,-1中,互为相反数的两个数是( )
| 1 |
| 3 |
| A、1与-2 | ||
| B、1与-1 | ||
C、-2与
| ||
D、
|
在“-22”中,底数指的是( )
| A、2 | B、-1 |
| C、-2 | D、22 |
 如图,在菱形ABCD中,对角线AC、BD相交于点O,已知AB=5cm,BD=8cm,求AC的长.
如图,在菱形ABCD中,对角线AC、BD相交于点O,已知AB=5cm,BD=8cm,求AC的长. 如图,在直角坐标系中,矩形OABC的顶点A、C在坐标轴上,点B(4,2);过点D(0,3)和E(6,0)的直线分别与AB、BC交于点M、N
如图,在直角坐标系中,矩形OABC的顶点A、C在坐标轴上,点B(4,2);过点D(0,3)和E(6,0)的直线分别与AB、BC交于点M、N 如图,∠A是⊙O的圆周角,∠A=42°,则∠OBC的度数为
如图,∠A是⊙O的圆周角,∠A=42°,则∠OBC的度数为 如图,平行四边形ABCD中,点E、F在对角线上,要使AE=CF,则需添加一个条件为
如图,平行四边形ABCD中,点E、F在对角线上,要使AE=CF,则需添加一个条件为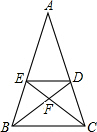 如图,等腰三角形△ABC,顶角∠A=36°,BD、CE分别是两个底角的平分线,交两腰分别于D、E两点,连接D、E,则在该图中,共有
如图,等腰三角形△ABC,顶角∠A=36°,BD、CE分别是两个底角的平分线,交两腰分别于D、E两点,连接D、E,则在该图中,共有