题目内容
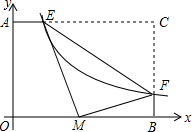 如图,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴、y轴建立平面直角坐标系.F是BC边上的点,过F点的反比例函数y=
如图,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴、y轴建立平面直角坐标系.F是BC边上的点,过F点的反比例函数y= (k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点M处,求点F的坐标.
(k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点M处,求点F的坐标.
 解:∵将△CEF沿EF对折后,C点恰好落在OB上的M点处,
解:∵将△CEF沿EF对折后,C点恰好落在OB上的M点处,∴∠EMF=∠C=90°,EC=EM,CF=MF,
∴∠MME+∠FMB=90°,
而EM⊥OB,
∴∠MME+∠MEM=90°,
∴∠MEM=∠FMB,
∴Rt△MEM∽Rt△BMF;
又∵EC=AC-AE=4-
 ,CF=BC-BF=3-
,CF=BC-BF=3- ,
,∴EM=4-
 ,MF=3-
,MF=3- ,
,∴
 =
= =
= ;
;∴ED:MB=EM:MF=4:3,而ED=3,
∴MB=
 ,
,在Rt△DBF中,MF2=MB2+MF2,即(3-
 )2=(
)2=( )2+(
)2+( )2,
)2,解得k=
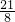 ,
,∴反比例函数解析式为y=
 ,
,把x=4代入得y=
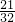 ,
,∴F点的坐标为(4,
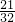 ).
).分析:过点E作ED⊥OB于点D,根据折叠的性质得∠EMF=∠C=90°,EC=EM,CF=DF,易证Rt△MEM∽Rt△BMF;而EC=AC-AE=4-
 ,CF=BC-BF=3-
,CF=BC-BF=3- ,得到EM=4-
,得到EM=4- ,MF=3-
,MF=3- ,即可得
,即可得 的比值;故可得出EM:MB=ED:MF=4:3,而ED=3,从而求出BM,然后在Rt△MBF中利用勾股定理得到关于k的方程,解方程求出k的值即可得到F点的坐标.
的比值;故可得出EM:MB=ED:MF=4:3,而ED=3,从而求出BM,然后在Rt△MBF中利用勾股定理得到关于k的方程,解方程求出k的值即可得到F点的坐标.点评:本题考查的是反比例函数综合题,涉及到反比例函数的性质、反比例函数图象上点的坐标特点,折叠的性质、勾股定理以及三角形相似的判定与性质等知识,难度适中.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
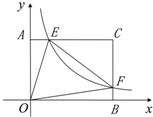 面直角坐标系.若点F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y=
面直角坐标系.若点F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y=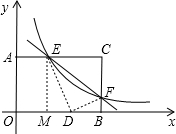 已知:在矩形AOBC中,OB=4,OA=3.分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数
已知:在矩形AOBC中,OB=4,OA=3.分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数 如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数
如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数 如图,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴、y轴建立平面直角坐标系.F是BC边上的点,过F点的反比例函数y=
如图,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴、y轴建立平面直角坐标系.F是BC边上的点,过F点的反比例函数y=