题目内容
如图，AB是⊙O 的一条直径，CD是⊙O的一条弦，交AB与点P， |
| AC |
|
| AD |
分析：连接OC，有条件可知CD⊥AB，再有垂径定理和勾股定理即可求出⊙O的直径．
解答：解：
连接OC，设OC=x，
∵
=
，
∴CD⊥AB，
∵CD=4，
∴CP=2，
∵AP=1，
∴OP=x-1，
在Rt△CPO中，
x2=22+（x-1）2，
解得：x=
，
∴⊙O的直径为2×
=5．
连接OC，设OC=x，∵
|
| AC |
|
| AD |
∴CD⊥AB，
∵CD=4，
∴CP=2，
∵AP=1，
∴OP=x-1，
在Rt△CPO中，
x2=22+（x-1）2，
解得：x=
| 5 |
| 2 |
∴⊙O的直径为2×
| 5 |
| 2 |
点评：本题考查了垂径定理以及垂径定理的推论和勾股定理的运用，解题的关键是连接圆心和圆上的一点构造直角三角形．
练习册系列答案
相关题目
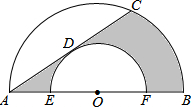如图，AB是半圆O的直径，以O为圆心，OE长为半径的半圆交AB于E、F两点，弦AC是小半圆的切线，D为切点，已知AO=4，EO=2，那么阴影部分的面积是
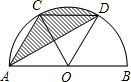如图，AB是半⊙O的直径，C、D是半圆的三等分点，半圆的半径为4．阴影部分的面积为
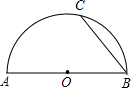cm，点O到BC的距离为4cm．
（2013•惠城区模拟）如图，AB是半圆⊙O的直径，弦CD∥AB，∠CAD=30°，若AB=6，则阴影部分的面积是
如图，AB是半圆O的直径，∠BAC=60°，D是半圆上任意一点，那么∠D的度数是（ ）