题目内容
如图,AB是半圆O的直径,BC是弦,点P从点A开始,沿AB向点B以1cm/s的速度移动,若AB长为10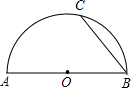 cm,点O到BC的距离为4cm.
cm,点O到BC的距离为4cm.(1)求弦BC的长;
(2)问经过几秒后△BPC是等腰三角形?
分析:(1)作OD⊥BC于D,易求得BC=2BD=6cm;
(2)由题意知,PB=AB=10-t,故有三种情况,BP=BC或PC=PB或BC=BP,分别求解.
(2)由题意知,PB=AB=10-t,故有三种情况,BP=BC或PC=PB或BC=BP,分别求解.
解答: 解:(1)作OD⊥BC于D,由垂径定理知,点D是BC的中点,BD=
解:(1)作OD⊥BC于D,由垂径定理知,点D是BC的中点,BD=
BC,
∵OB=
AB=5,OD=4,
由勾股定理得,BD=
=3,
∴BC=2BD=6cm;
(2)设经过t秒后,△BPC是等腰三角形,
①当PC为底边时,有BP=BC,10-t=6,解得:t=4(秒);
②当BC为底边时,有PC=PB,P点与O点重合,此时t=5(秒);
③当PB为底边时,有PC=BC,连接AC,作CE⊥AB于E,
则BE=
,AE=
,
∵AB是直径,
∴△ABC是直角三角形,
根据勾股定理AC=
=
=8,
由AC2-AE2=BC2-BE2,
64-(
)2=36-(
)2,
解得:t=2.8(秒).
综上,经过4秒或5秒或2.8秒时,△BPC是等腰三角形.
 解:(1)作OD⊥BC于D,由垂径定理知,点D是BC的中点,BD=
解:(1)作OD⊥BC于D,由垂径定理知,点D是BC的中点,BD=| 1 |
| 2 |
∵OB=
| 1 |
| 2 |
由勾股定理得,BD=
| OB2-OD2 |
∴BC=2BD=6cm;
(2)设经过t秒后,△BPC是等腰三角形,
①当PC为底边时,有BP=BC,10-t=6,解得:t=4(秒);
②当BC为底边时,有PC=PB,P点与O点重合,此时t=5(秒);
③当PB为底边时,有PC=BC,连接AC,作CE⊥AB于E,
则BE=
| 10-t |
| 2 |
| 10+t |
| 2 |
∵AB是直径,

∴△ABC是直角三角形,
根据勾股定理AC=
| AB2-BC2 |
| 102-62 |
由AC2-AE2=BC2-BE2,
64-(
| 10+t |
| 2 |
| 10-t |
| 2 |
解得:t=2.8(秒).
综上,经过4秒或5秒或2.8秒时,△BPC是等腰三角形.
点评:本题利用了垂径定理,勾股定理求解,注意当△BPC是等腰三角形时,点P的位置有三种情况.

练习册系列答案
相关题目
 如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.
如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm. 已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C.
已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C. 如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是
如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
