Question

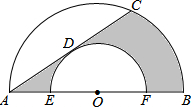如图，AB是半圆O的直径，以O为圆心，OE长为半径的半圆交AB于E、F两点，弦AC是小半圆的切线，D为切点，已知AO=4，EO=2，那么阴影部分的面积是

 

．

Answer 1

分析：阴影部分的面积可以看作是△AOC的面积加上扇形BOC的面积减去半圆EOF的面积．

解答：解：连接OD，OC，则OD⊥AC．
∵AO=4，EO=2，
∴cos∠AOD=cos∠COD=

1

2

，
∴∠AOD=∠COD=60°，
∴∠COB=180°-60°-60°=60°，
阴影部分面积为：

1

2

×4×2×sin60°×2+

60

360

π×4²-

1

2

π×2²=4

3

+

2

3

π．
故答案为：4

3

+

2

3

π．

点评：求不规则的图形的面积，可以转化为几个规则图形的面积的和或差来求．