题目内容
小明在公路上骑摩托车，上午8：00时看到公路上的里程碑是二位数，十位上的数字是a，个位上的数字是b，到上午9：00时看到公路上的里程碑上的数还是原来的二个数字，顺序也和原来一样，只不过中间多了个0，小明骑摩托车的速度是 km∕h．
考点：一元一次方程的应用
专题：
分析：由题意，可知小明上午8：00时看到的两位数为10a+b，行驶一小时后看到的两位数为100a+b，根据速度=路程÷时间即可求解．
解答：解：∵小明上午8：00时看到的两位数为10a+b，行驶一小时后看到的两位数为100a+b，
∴小明骑摩托车的速度是：（100a+b-10a-b）÷（9-8）=90a（km∕h）．
故答案为90a．
∴小明骑摩托车的速度是：（100a+b-10a-b）÷（9-8）=90a（km∕h）．
故答案为90a．
点评：本题考查了列代数式，正确地表示小明上午8：00及9：00时看到的两位数是解题的关键．
练习册系列答案
相关题目
如图，在周长为30cm的?ABCD中，AB＜AD，AC、BD相交于点O，OE⊥BD交AD于点E，则△ABE的周长为用配方法将关于x的方程x2+5x+n=0可以变形为（x+p）2=9，那么用配方法也可以将关于x的方程x2-5x+n=-1变形为下列形式（ ）
| A、（x-p+1）2=10 |
| B、（x-p）2=8 |
| C、（x-p-1）2=8 |
| D、（x-p）2=10 |
如图，四边形ABCD，∠A=130°，点D在AB、AC的垂直平分线上，则∠BDC=（ ）| A、90° | B、100° |
| C、120° | D、130° |
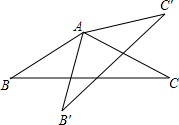已知：如图，△ABC中，∠C=26°，绕点A旋转△ABC，旋转后，B、C两点分别记作B′，C′，并且B′C′∥AB，AB′⊥AC，你能用学过的数学知识解决△ABC绕点A转过的角是多少度吗？