题目内容
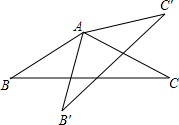 已知:如图,△ABC中,∠C=26°,绕点A旋转△ABC,旋转后,B、C两点分别记作B′,C′,并且B′C′∥AB,AB′⊥AC,你能用学过的数学知识解决△ABC绕点A转过的角是多少度吗?
已知:如图,△ABC中,∠C=26°,绕点A旋转△ABC,旋转后,B、C两点分别记作B′,C′,并且B′C′∥AB,AB′⊥AC,你能用学过的数学知识解决△ABC绕点A转过的角是多少度吗?考点:旋转的性质
专题:
分析:先根据图形旋转的性质得出∠C′=∠C,∠C′AC=∠BAB′,再平行线的性质得出∠B=∠BAB′,故∠B=∠C′AC,再根据三角形的内角和定理即可得出结论.
解答:解:∵△A′B′C′由△ABC旋转而成,
∴∠C′=∠C=26°,∠C′AC=∠BAB′,
∵B′C′∥AB,
∴∠B′=∠BAB′,
∴∠B′=∠C′AC,
∵AB′⊥AC,
∴∠B′AC=90°,
在△B′AC中,
∵∠B′+∠B′AC+∠C=180°,即2∠B′+∠B′AC+∠C′=180°,即2∠B′+90°+26°=180°,
解得∠B′=32°,即△ABC绕点A转过的角是32度.
∴∠C′=∠C=26°,∠C′AC=∠BAB′,
∵B′C′∥AB,
∴∠B′=∠BAB′,
∴∠B′=∠C′AC,
∵AB′⊥AC,
∴∠B′AC=90°,
在△B′AC中,
∵∠B′+∠B′AC+∠C=180°,即2∠B′+∠B′AC+∠C′=180°,即2∠B′+90°+26°=180°,
解得∠B′=32°,即△ABC绕点A转过的角是32度.
点评:本题考查的是旋转的性质,熟知图形旋转不变性的性质是解答此题的关键.

练习册系列答案
相关题目
分解因式a2-2a+1-b2正确的是( )
| A、(a-1)2-b2 |
| B、a(a-2)-(b+1)(b-1) |
| C、(a+b-1)(a-b-1) |
| D、(a+b)(a-b)-2a+1 |
不等式4x+3≤3x+5的非负整数解的个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,在Rt△ABC中,斜边AB过⊙O的圆心,∠BAC的平分线交BC于⊙O上的点D,AB交⊙O于点E.
如图,在Rt△ABC中,斜边AB过⊙O的圆心,∠BAC的平分线交BC于⊙O上的点D,AB交⊙O于点E.
 如图,在△ABC中,∠A=70°,∠ABC、∠ACB的平分线OB、OC相交于O.求∠BOC的度数.
如图,在△ABC中,∠A=70°,∠ABC、∠ACB的平分线OB、OC相交于O.求∠BOC的度数.