Question

2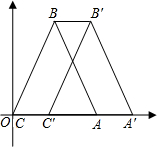．如图，在平面直角坐标系中，△ABC是等腰三角形，BC=BA，B点坐标为（1，$\sqrt{3}$），C点坐标为（0，0），且S_△ABC=$\sqrt{3}$．将△ABC沿x轴向右平移$\sqrt{2}$个单位长，使点A、B、C分别平移到A′，B′，C′．
（1）求A点的坐标；
（2）写出A′，B′，C′三点的坐标；
（3）求平行四边形AA′B′B的面积．

Answer 1

分析 （1）根据B点坐标和S_△ABC=$\sqrt{3}$，求出AC的长，得到A点的坐标；
（2）根据平移变换的性质写出A′，B′，C′三点的坐标；
（3）根据平行四边形的面积公式和点的坐标特征可求出平行四边形AA′B′B的面积．

解答 解：（1）∵B点坐标为（1，$\sqrt{3}$），C点坐标为（0，0），且S_△ABC=$\sqrt{3}$，
∴$\frac{1}{2}$×AC×$\sqrt{3}$=$\sqrt{3}$，
解得，AC=2，
∴A点的坐标为（2，0）；
（2）A′（2+$\sqrt{2}$，0），B′（1+$\sqrt{2}$，$\sqrt{3}$），C′（$\sqrt{2}$，0）；
（3）平行四边形AA′B′B的面积=AA′×$\sqrt{3}$=$\sqrt{6}$．

点评 本题考查的是等腰三角形的性质、平行四边形的面积的计算和平移变换，掌握平移变换的性质和坐标与图形的关系是解题的关键．