题目内容
3. 如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,AB=2cm,以点C为圆心,r长为半径画圆,使点B在⊙C外,点D在⊙C内,求半径r的取值范围.
如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,AB=2cm,以点C为圆心,r长为半径画圆,使点B在⊙C外,点D在⊙C内,求半径r的取值范围.
分析 根据条件求出BC、CD的长即可解决问题.
解答 解:∵∠ACB=90°,∠A=30°,CD⊥AB,AB=2cm,
∴BC=$\frac{1}{2}$AB=1,BD=$\frac{1}{2}$BC=$\frac{1}{2}$,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\frac{\sqrt{3}}{2}$.
∴当$\frac{\sqrt{3}}{2}$<r<1时,点B在⊙C外,点D在⊙C内.
点评 本题考查点与圆的位置关系、直角三角形30度角性质,勾股定理等知识,解题的关键是熟练掌握点圆的位置关系的判定,属于中考常考题型.

练习册系列答案
相关题目
11.一元二次方程x2-16=0的根是( )
| A. | x=2 | B. | x=4 | C. | x1=2,x2=-2 | D. | x1=4,x2=-4 |
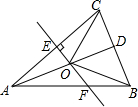 如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( ) 如图.已知:△ABC≌△EFC,且CF=5cm,∠EFC=52°,求∠A的度数和BC的长.
如图.已知:△ABC≌△EFC,且CF=5cm,∠EFC=52°,求∠A的度数和BC的长.
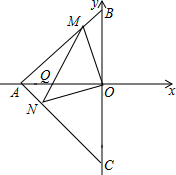 已知A(-4,0),B(0,4),C(0,-4),过O作OM⊥ON交AB、AC于M、N两点
已知A(-4,0),B(0,4),C(0,-4),过O作OM⊥ON交AB、AC于M、N两点