Question

如图①，△ABC的角平分线BD、CE相交于点P. 

   （1）如果∠A=70°，求∠BPC的度数；

   （2）如图②，过P点作直线MN∥BC，分别交AB和AC于点M和N，试求

       ∠MPB+∠NPC的度数（用含∠A的代数式表示）；

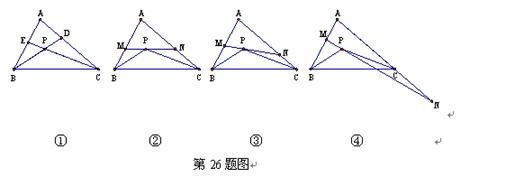
（3）在（2）的条件下，将直线MN绕点P旋转.

        （i）当直线MN与AB、AC的交点仍分别在线段AB和AC上时，如图③，

试探索∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由；

       （ii）当直线MN与AB的交点仍在线段AB上，而与AC的交点在AC的

            延长线上时，如图④，试问（i）中∠MPB、∠NPC、∠A三者之间

            的数量关系是否仍然成立？若成立，请说明你的理由；若不成立，请

            给出∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由.           

Answer 1

（1）125°（3分）；（2）利用平行线的性质求解或先说明∠BPC=90°+∠A，∴∠MPB+∠NPC=180°-∠BPC=180°-（90°+∠A）=90°-∠A（3分）；（3）（每小题4分）（i）∠MPB+∠NPC= 90°-∠A（2分）.理由：先说明∠BPC=90°+∠A，则∠MPB+∠NPC=180°-∠BPC=180°-(90°+∠A)= 90°-∠A（2分）；（ii）不成立（1分），∠MPB-∠NPC=90°-∠A（1分）.理由：由图可知∠MPB+∠BPC-∠NPC=180°，由（i）知：∠BPC=90°+∠A，∴∠MPB-∠NPC=180°-∠BPC=180°-(90°+∠A)= 90°-∠A（2分）.