题目内容
设正三角形ABC的边长为2，M是AB边上的中点，P是边BC上的任意一点，PA+PM的最大值和最小值分别记为s和t，则s2-t2=________．
4
分析：先M关于BC的对称点M′与A的连线AM′与BC交点时PA+PM取最小值t，当P与C重合时为最大值s，再根据特殊角的三角函数值及勾股定理分别求出s、t的值即可．
解答：
解：如图，作M关于BC的对称点M′与A的连线AM′与BC交点时PA+PM取最小值t，
当P与C重合时为最大值s=2+，
过A作AD⊥M′M交其延长线于D，易知M′D=3MH=
，
又因为AD=
，所以PM+PA=PM′+PA=AM′=
（勾股定理），
故s-t=2+-，
s2-t2=4．
故答案为：4．
点评：本题考查的是最短路线问题，根据题意分别作出各点的对称点，即辅助线是解答此题的关键．
分析：先M关于BC的对称点M′与A的连线AM′与BC交点时PA+PM取最小值t，当P与C重合时为最大值s，再根据特殊角的三角函数值及勾股定理分别求出s、t的值即可．
解答：
解：如图，作M关于BC的对称点M′与A的连线AM′与BC交点时PA+PM取最小值t，当P与C重合时为最大值s=2+
，过A作AD⊥M′M交其延长线于D，易知M′D=3MH=
，又因为AD=
，所以PM+PA=PM′+PA=AM′=（勾股定理），故s-t=2+
-，s2-t2=4
．故答案为：4
．点评：本题考查的是最短路线问题，根据题意分别作出各点的对称点，即辅助线是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
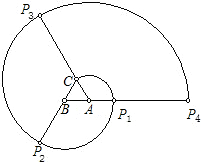
如图，正三角形ABC的边长为1cm，将线段AC绕点A顺时针旋转120°至AP1，形成扇形D1；将线段BP1绕点B顺时针旋转120°至BP2，形成扇形D2；将线段CP2绕点C顺时针旋转120°至CP3，形成扇形D3；将线段AP3绕点A顺时针旋转120°至AP4，形成扇形D4…．设ln为扇形Dn的弧长（n=1，2，3…），回答下列问题：
（1）按照要求填表：
（2）根据上表所反映的规律，试估计n至少为何值时，扇形Dn的弧长能绕地球赤道一周（设地球赤道半径为6400km）．
（1）按照要求填表：
| n | 1 | 2 | 3 | 4 |
| ln |
________．