题目内容
设正三角形ABC的边长为2,M是AB边上的中点,P是BC上任意一点,PA+PM的最大值和最小值分别记为s和t,则s2-t2=________.
答案:
解析:
解析:
|
如图,由于P是BC上任意一点,要使PA+PM最大,只有P与C重合,这时
s=CM+CA = = =2+ 要使PA+PM最小,需作M关于BC的对称点 ∵BC是M ∴C ∠BC ∴AC ∴t= = ∴s2-t2=(2+ = |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,正三角形ABC的边长为1cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4….设ln为扇形Dn的弧长(n=1,2,3…),回答下列问题:
(1)按照要求填表:
(2)根据上表所反映的规律,试估计n至少为何值时,扇形Dn的弧长能绕地球赤道一周(设地球赤道半径为6400km).
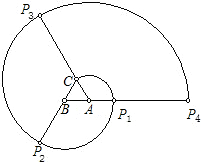
(1)按照要求填表:
| n | 1 | 2 | 3 | 4 |
| ln |



 ________.
________.