Question

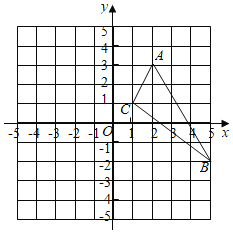
【题目】已知如图，在中，三个顶点的坐标分别为，将沿 轴负方向平移个单位长度，再沿轴负方向平移个单位长度，得到，其 中点的对应点为点，点的对应点为点，点的对应点为点

直接写出平移后的的顶点坐标：

在坐标系中画出平移后的

求出的面积．

Answer 1

【答案】（1）；；；（2）详见解析；（3）5

【解析】

（1）已知，将沿 轴负方向平移个单位长度，再沿轴负方向平移个单位长度，得到，根据直角坐标系中坐标平移特点，A点横坐标减去4，纵坐标减2．即可得到D点坐标，同理得到E、F点坐标．

（2）已知D(-2,1)，E(1,-3)，F(-3,-1)，在直角坐标系中标注出D、E、F三点坐标，再连接DF，DE，EF，即可得到△DEF．

（3）由已知，，S△DEF=S矩形CGHE-S△DFG- S△DCE，即可求解．

（1）∵，将A沿 轴负方向平移个单位长度，再沿轴负方向平移个单位长度得到点D

∵2-4=-2，3-2=1

∴点坐标为(-2,1)

∵，将A沿 轴负方向平移个单位长度，再沿轴负方向平移个单位长度得到点E

∵5-4=1，-1-2=-3

∴点坐标为(1,-3)

∵，将A沿 轴负方向平移个单位长度，再沿轴负方向平移个单位长度得到点F

∵1-4=-3，1-2=-1

∴点坐标为(-3,-1)

∴D(-2,1)，E(1,-3)，F(-3,-1)

故答案为：D(-2,1)，E(1,-3)，F(-3,-1)

（2）已知D(-2,1)，E(1,-3)，F(-3,-1)，在直角坐标系中标注出D、E、F三点坐标，再连接DF，DE，EF，如图所示得到△DEF．

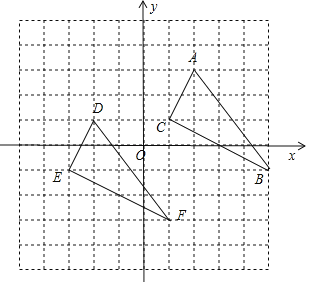
（3）∵

∴S△DEF=S矩形CGHE-S△DFG-S△HFE-S△DCE

故答案为：5