题目内容
4.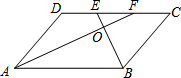 如图,在?ABCD中,AD=4,AB=6,∠BAD,∠ABC的平分线交于点O,且分别交DC于F,E,则S△EOF:S△AOB=( )
如图,在?ABCD中,AD=4,AB=6,∠BAD,∠ABC的平分线交于点O,且分别交DC于F,E,则S△EOF:S△AOB=( )| A. | 1:9 | B. | 2:3 | C. | 1:3 | D. | 4:9 |
分析 由四边形ABCD是平行四边形,可得AB∥CD,CD=AB=6,BC=AD=4,又由AF是∠BAD的平分线,BE是∠ABC的平分线,易证得△ADF与△BCE是等腰三角形,继而求得EF的长,然后由相似三角形的面积比等于相似比的平方求得答案.
解答 解:∵四边形BCD是平行四边形,
∴AB∥CD,CD=AB=6,BC=AD=4,
∴∠DFA=∠FAB,
∵AF是∠BAD的平分线,
∴∠DAF=∠FAB,
∴∠DFA=∠DAF,
∴DF=AD=4,
同理:CE=BC=4,
∴EF=DF+CF-CD=4+4-6=2,
∵△EOF∽△BOA,
∴S△EOF:S△AOB=($\frac{EF}{AB}$)2=($\frac{1}{3}$)2=$\frac{1}{9}$.
故选A.
点评 此题考查了平行四边形的性质,相似三角形的判定与性质以及等腰三角形的判定与性质等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
13.在平面直角坐标系中,点坐标为(-3,4),则P点所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
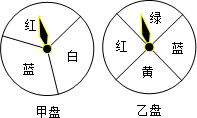 张老师为了激发学生的学习兴趣,设计一个“配紫色”游戏.如图是两个可以自由转动的转盘,每个转盘被分成大小相等的几个扇形.转盘甲中的扇形分别涂有红、蓝、白三种颜色,转盘乙中的扇形分别涂有黄、绿、蓝、红四种颜色.游戏者同时转动两个转盘,如果转盘停止后,一个转盘的指针指向红色,另一个转盘的指针指向蓝色,那么红色和蓝色在一起就配成了紫色(若指针指向扇形的分界线,则需重新转动).
张老师为了激发学生的学习兴趣,设计一个“配紫色”游戏.如图是两个可以自由转动的转盘,每个转盘被分成大小相等的几个扇形.转盘甲中的扇形分别涂有红、蓝、白三种颜色,转盘乙中的扇形分别涂有黄、绿、蓝、红四种颜色.游戏者同时转动两个转盘,如果转盘停止后,一个转盘的指针指向红色,另一个转盘的指针指向蓝色,那么红色和蓝色在一起就配成了紫色(若指针指向扇形的分界线,则需重新转动).