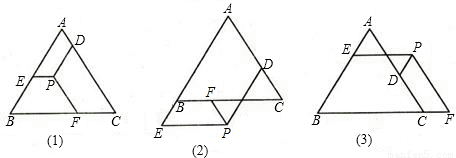
题目内容
已知：点P是正△ABC内任意一点，过点P分别作PD∥AB交直线AC于D，PE∥BC交直线AB于E，PF∥AC交直线BC于F，如图（1），易证：PE+PF+PD=AB．若点P在正△ABC外部如图（2）、图（3）时，其它条件不变，试猜想PD、PE、PF、AB之间的数量关系，并对其中一种猜想给出证明．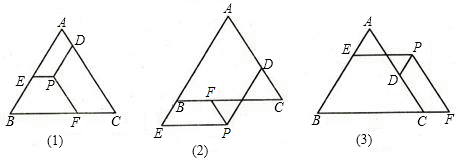
解：图（2）结论：PD+PE-PF=AB
证明如下：如图，延长PF交AB于K，易证PE=EK，PF=BE，PD=AK
∵AB=AK+EK-BE
∴AB=PD+PE-PF
图（3）结论：PE+PF-PD=AB．
分析：先写出正确的结论，选择其中的一种加以证明．如图（2），延长PF交AB于K，根据平行线的性质，证得PE=EK，PF=BE，PD=AK，从而得到正确的结论．
点评：本题考查了等边三角形和平行线的性质；作出辅助线是正确解答本题的关键．
证明如下：如图，延长PF交AB于K，易证PE=EK，PF=BE，PD=AK
∵AB=AK+EK-BE
∴AB=PD+PE-PF
图（3）结论：PE+PF-PD=AB．
分析：先写出正确的结论，选择其中的一种加以证明．如图（2），延长PF交AB于K，根据平行线的性质，证得PE=EK，PF=BE，PD=AK，从而得到正确的结论．
点评：本题考查了等边三角形和平行线的性质；作出辅助线是正确解答本题的关键．
练习册系列答案
相关题目
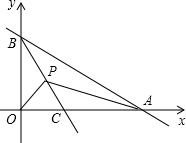如图，已知A，B两点是直线AB与x轴的正半轴，y轴的正半轴的交点，且OA，OB的长分别是x2-14x+48=0的两个根（OA＞OB），射线BC平分∠ABO交x轴于C点，若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动，运动时间为t秒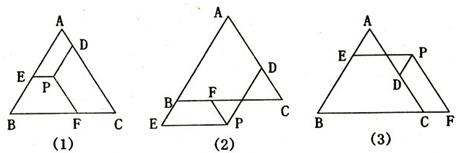
已知a，b是正实数，