题目内容
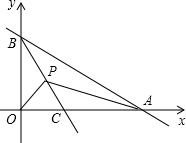 如图,已知A,B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,且OA,OB的长分别是x2-14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒
如图,已知A,B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,且OA,OB的长分别是x2-14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒(1)设△APB和△OPB的面积分别为S1,S2,求S1:S2;
(2)求直线BC的解析式;
(3)在点P的运动过程中,△OPB可能是等腰三角形吗?若可能,求出时间t;若不可能,请说明理由.
分析:(1)先求出OA和OB的长度,P是角平分线上的点,P到OB,AB的距离相等,而两个三角形的高相等,S1:S2=AB:OB=5:3;
(2)过C作CD垂直AB,垂足为D,设OC=x,则CD=x,易知BD=OB,然后根据勾股定理列出方程式解答即可;
(3)分别取三个点做顶角的顶点,然后求出符合题意的t的值.
(2)过C作CD垂直AB,垂足为D,设OC=x,则CD=x,易知BD=OB,然后根据勾股定理列出方程式解答即可;
(3)分别取三个点做顶角的顶点,然后求出符合题意的t的值.
解答:解:(1)x2-14x+48=0 x1=6,x2=8; OA=8,OB=6 AB=10(3分)
P是角平分线上的点,P到OB,AB的距离相等,
S1:S2=AB:OB=5:3,
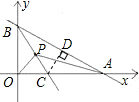
(2)过C作CD垂直AB,垂足为D,
设OC=x,则CD=x,易知BD=OB,
在直角三角形CDA中:CD2+AD2=AC2,
x2+42=(8-x)2
x=3(7分)
所以C点的坐标(3,0)
BC的解析式:y=-2x+6(9分)
(3)①BP=OB时,t=6(10分)
②BP=OP时,P在OB的中垂线上,yp=3,代入直线BC的解析式得P(
,3),
利用勾股定理可得BP=
③OB=OP时,t=
.(12分)
P是角平分线上的点,P到OB,AB的距离相等,
S1:S2=AB:OB=5:3,

(2)过C作CD垂直AB,垂足为D,
设OC=x,则CD=x,易知BD=OB,
在直角三角形CDA中:CD2+AD2=AC2,
x2+42=(8-x)2
x=3(7分)
所以C点的坐标(3,0)
BC的解析式:y=-2x+6(9分)
(3)①BP=OB时,t=6(10分)
②BP=OP时,P在OB的中垂线上,yp=3,代入直线BC的解析式得P(
| 3 |
| 2 |
利用勾股定理可得BP=
3
| ||
| 2 |
③OB=OP时,t=
24
| ||
| 5 |
点评:本题主要考查对与勾股定理和一元二次方程的应用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
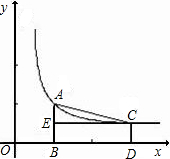 如图,已知A、C两点在双曲线y=
如图,已知A、C两点在双曲线y= (2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是
(2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是 如图,已知A、B两点的坐标分别为(
如图,已知A、B两点的坐标分别为( 如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.
如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论. 如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.
如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.