题目内容
 如图,AD=AE,AB=AC,CD与BE相交于点F,则图中的全等三角形一共有( )
如图,AD=AE,AB=AC,CD与BE相交于点F,则图中的全等三角形一共有( )分析:认真观察图形,确定已知条件在图形上的位置,结合全等三角形的判定方法,由易到难,仔细寻找.
解答:解:∵在△AEB和△ADC中
,
∴△AEB≌△ADC(SAS),
∴CE=BD,∠B=∠C,
在△BDF和△CEF中
,
∴△BDF≌△CEF(AAS),
∴BF=CF,
在△AFC和△AFB中
,
∴△AFC≌△AFB(SSS),
∴∠BAF=∠CAF,
在△DAF和△EAF中
,
∴△DAF≌△EAF(SAS),
∴图中全等三角形共4对.
故选:D.
|
∴△AEB≌△ADC(SAS),
∴CE=BD,∠B=∠C,
在△BDF和△CEF中
|
∴△BDF≌△CEF(AAS),

∴BF=CF,
在△AFC和△AFB中
|
∴△AFC≌△AFB(SSS),
∴∠BAF=∠CAF,
在△DAF和△EAF中
|
∴△DAF≌△EAF(SAS),
∴图中全等三角形共4对.
故选:D.
点评:此题主要考查了全等三角形的判定,全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
相关题目
 2、如图,AD=AE,∠1=∠2,BD=CE,则有△ABD≌△
2、如图,AD=AE,∠1=∠2,BD=CE,则有△ABD≌△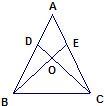 21、已知:如图,AD=AE,∠ADC=∠AEB,BE与CD相交于O点.
21、已知:如图,AD=AE,∠ADC=∠AEB,BE与CD相交于O点. 39、已知:如图,AD=AE,AB=AC,BD、CE相交于O.
39、已知:如图,AD=AE,AB=AC,BD、CE相交于O. 23、已知:如图,AD=AE,AB=AC,DC与BE交于O点.
23、已知:如图,AD=AE,AB=AC,DC与BE交于O点. 如图,AD=AE,AB=AC,∠A=60°,∠C=25°,则∠DOB=
如图,AD=AE,AB=AC,∠A=60°,∠C=25°,则∠DOB=