题目内容
反比例函数 (k>0)与一次函数
(k>0)与一次函数 (b>0)的图像相交于两点
(b>0)的图像相交于两点 ,线段AB交y轴于点C,当
,线段AB交y轴于点C,当 且AC=2BC时,k、b的值分别为( ).
且AC=2BC时,k、b的值分别为( ).
A.k= ,b=2 ,b=2 | B.k= ,b=1 ,b=1 | C.k= ,b= ,b= | D.k= ,b= ,b= |
D
解析试题分析:首先由AC=2BC,可得出A点的横坐标的绝对值是B点横坐标绝对值的两倍.再由 ,可求出A点与B点的横坐标,然后根据点A、点B既在一次函数
,可求出A点与B点的横坐标,然后根据点A、点B既在一次函数 的图象上,又在反比例函数
的图象上,又在反比例函数 (k>0)的图象上,可求出k、b的值.
(k>0)的图象上,可求出k、b的值.
∵AC=2BC,
∴A点的横坐标的绝对值是B点横坐标绝对值的两倍.
∵点A、点B都在一次函数 的图象上,
的图象上,
∴可设B(m,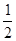 m+b),则A(-2m,-m+b).
m+b),则A(-2m,-m+b).
∵
∴m-(-2m)=2,解得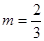
又∵点A、点B都在反比例函数 (k>0)的图象上,
(k>0)的图象上,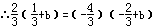
解得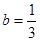
∴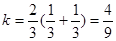
故选D.
考点:反比例函数、一次函数的性质
点评:此题难度稍大,综合性比较强,注意对各个知识点的灵活应用,注意通过解方程组求出k、b的值.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
若点(3,4)是反比例函数y=
的图象上一点,则此函数图象必经过点( )
| m2+2m+1 |
| x |
| A、(2,6) |
| B、(-2.6) |
| C、(4,-3) |
| D、(3,-4) |




 如图,点A在反比例函数y=
如图,点A在反比例函数y= 若一次函数y=kx+b的图象如图所示,则抛物线y=x2+kx+b的对称轴位于y轴的
若一次函数y=kx+b的图象如图所示,则抛物线y=x2+kx+b的对称轴位于y轴的