题目内容
12．
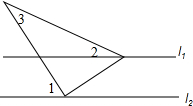如图，直线l1∥l2，∠1=50°，∠2=23°20′，则∠3的度数为（ ）| A． | 27°20′ | B． | 26°40′ | C． | 27°40′ | D． | 73°20′ |
分析 根据平行线的性质求得∠4的度数，然后根据三角形的外角等于不相邻的内角的和求解．
解答 
解：∵l1∥l2，
∴∠4=∠1=50°，
又∵∠4=∠3+∠2，
∴∠3=∠4-∠2=50°-23°20′=26°40′．
故选B．
点评 本题考查了平行线的性质以及三角形的外角的性质：三角形的外角等于不相邻的两个内角的和，理解性质是关键．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
3．
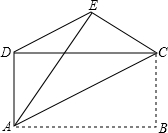如图，已知四边形ABCD是矩形，把矩形沿直线AC折叠，点B落在点E处，连接DE．若DE：AC=3：5，则$\frac{AD}{AB}$的值为（ ）
如图，已知四边形ABCD是矩形，把矩形沿直线AC折叠，点B落在点E处，连接DE．若DE：AC=3：5，则$\frac{AD}{AB}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{2}}{2}$ |
20．
如图，O为原点，数轴上A，B，O，C四点，表示的数与点A所表示的数是互为相反数的点是（ ）
如图，O为原点，数轴上A，B，O，C四点，表示的数与点A所表示的数是互为相反数的点是（ ）| A． | 点B | B． | 点O | C． | 点A | D． | 点C |
7．3x2可能表示为（ ）
| A． | x2+x2+x2 | B． | x2•x2•x2 | C． | 3x•3x | D． | 9x |
17．对于反比例函数y=$\frac{k}{x}$（k≠0），下列说法正确的是（ ）
| A． | 当k＞0时，y随x增大而增大 | |
| B． | 当k＜0时，y随x增大而增大 | |
| C． | 当k＞0时，该函数图象在二、四象限 | |
| D． | 若点（1，2）在该函数图象上，则点（2，1）也必在该函数图象上 |
4．
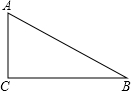如图，△ABC中，∠C=90°，则∠A的余弦值可以表示为（ ）
如图，△ABC中，∠C=90°，则∠A的余弦值可以表示为（ ）| A． | $\frac{AC}{AB}$ | B． | $\frac{AC}{BC}$ | C． | $\frac{BC}{AB}$ | D． | $\frac{BC}{AC}$ |
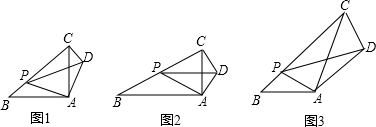
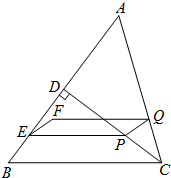如图，在△ABC中，AC=BC=5cm，AB=6cm，CD⊥AB于点D．动点P，Q同时从点C出发，点P沿线CD做依次匀速往返运动，回到点C停止；点Q沿折线CA-AD向终点D做匀速运动；点P，Q运动的速度都是5cm/s．过点P作PE∥BC，交AB于点E，连接PQ．当点P，E不重合且点P，Q不重合时，以线段PE，PQ为一组邻边作□PEFQ．设点P运动的时间为t（s），?PEFQ与△ABC重叠部分的面积为S（cm2）．