题目内容
12. 如图,已知△ABC中,AB=AC=20厘米,BC=16厘米,点D为AB的中点.如果点P在线段BC上以6厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①设点P运动的时间为t,用含有t的代数式表示线段PC的长度;②若点Q的运动速度与点P的运动速度相等,经过t秒后,△BPD与△CQP是否全等,求t的值.
如图,已知△ABC中,AB=AC=20厘米,BC=16厘米,点D为AB的中点.如果点P在线段BC上以6厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①设点P运动的时间为t,用含有t的代数式表示线段PC的长度;②若点Q的运动速度与点P的运动速度相等,经过t秒后,△BPD与△CQP是否全等,求t的值.
分析 ①先表示出BP,根据PC=BC-BP,可得出答案;
②分类讨论,当△BPD≌△CPQ和△BPD≌△CQP时,由全等三角形的性质就可以求出结论.
解答 解:①BP=6t,则PC=BC-BP=16-6t;
②当△BPD≌△CPQ时,
BP=CP.
∵BP+CP=BC=16厘米,
∴BP=8,
∴t=$\frac{4}{3}$;
当△BPD≌△CQP时,
BD=CP.
∵点D为AB的中点,
∴BD=$\frac{1}{2}$AB.
∵AB=20,
∴BD=10,
∴CP=10,
∴BP=6,
∴t=1.
故经过1或 $\frac{4}{3}$秒后,△BPD与△CQP全等.
点评 本题考查了动点问题在实际生活中的运用,全等三角形的性质的运用,行程问题的数量关系的运用,解答时运用全等三角形的性质求解是关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
20.Rt△ABC中,∠C=90°,AC=3,CB=4,给出下列三个结论:
①以点C为圆心,1.3长为半径的圆与AB相离;
②以点C为圆心,2.4长为半径的圆与AB相切;
③以点C为圆心,2.5长为半径的圆与AB相交.
上述结论正确的个数是( )
①以点C为圆心,1.3长为半径的圆与AB相离;
②以点C为圆心,2.4长为半径的圆与AB相切;
③以点C为圆心,2.5长为半径的圆与AB相交.
上述结论正确的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
7. 某商店今年1-6月份经营A、B两种电子产品,已知A产品每个月的销售数量y(件)与月份x(1≤x≤6且x为整数)之间的关系如表:
某商店今年1-6月份经营A、B两种电子产品,已知A产品每个月的销售数量y(件)与月份x(1≤x≤6且x为整数)之间的关系如表:
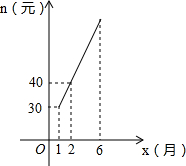
A产品每个月的售价z(元)与月份x之间的函数关系式为:z=10x;已知B产品每个月的销售数量m(件)与月份x之间的关系为:m=-2x+62,B产品每个月的售价n(元)与月份x之间存在如图所示的变化趋势;
(1)请观察题中表格,用所学过的一次函数或反比例函数的有关知识,直接写出y与x的函数关系式;
(2)请观察如图所示的变化趋势,求出n与x的函数关系式;
(3)求出商店1-6月份经营A、B两种电子产品的销售总额w与月份x之间的函数关系式;
(4)今年7月份,商店调整了A、B两种电子产品的价格,A产品价格在6月份基础上增加a%,B产品价格在6月份基础上减少a%,结果7月份A产品的销售数量比6月份减少2a%,B产品的销售数量比6月份增加2a%.若调整价格后7月份的销售总额比6月份的销售总额少2000元,请根据以下参考数据估算a的值.
(参考数据:6.32=39.69,6.42=40.91,6.52=42.25,6.62=43.56)
 某商店今年1-6月份经营A、B两种电子产品,已知A产品每个月的销售数量y(件)与月份x(1≤x≤6且x为整数)之间的关系如表:
某商店今年1-6月份经营A、B两种电子产品,已知A产品每个月的销售数量y(件)与月份x(1≤x≤6且x为整数)之间的关系如表:| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 600 | 300 | 200 | 150 | 120 | 100 |
(1)请观察题中表格,用所学过的一次函数或反比例函数的有关知识,直接写出y与x的函数关系式;
(2)请观察如图所示的变化趋势,求出n与x的函数关系式;
(3)求出商店1-6月份经营A、B两种电子产品的销售总额w与月份x之间的函数关系式;
(4)今年7月份,商店调整了A、B两种电子产品的价格,A产品价格在6月份基础上增加a%,B产品价格在6月份基础上减少a%,结果7月份A产品的销售数量比6月份减少2a%,B产品的销售数量比6月份增加2a%.若调整价格后7月份的销售总额比6月份的销售总额少2000元,请根据以下参考数据估算a的值.
(参考数据:6.32=39.69,6.42=40.91,6.52=42.25,6.62=43.56)
17.关于一次函数y=2x-1,下列说法中,正确的是( )
| A. | 图象经过第二象限 | B. | 函数值y随x的增大而减小 | ||
| C. | 图象在x轴上的截距是1 | D. | 图象在y轴上的截距是-1 |
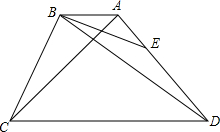 如图,AB∥CD,∠CBE=∠CAD=90°.AC=AD=6,DE=4,则BD长为2$\sqrt{17}$.
如图,AB∥CD,∠CBE=∠CAD=90°.AC=AD=6,DE=4,则BD长为2$\sqrt{17}$.
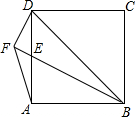 如图,四边形ABCD是正方形,点E是边AD上一点,DF⊥BE,交BE的延长线于点F,连接AF.若DF=1,AF=$\sqrt{2}$,则BD的长是$\sqrt{10}$.
如图,四边形ABCD是正方形,点E是边AD上一点,DF⊥BE,交BE的延长线于点F,连接AF.若DF=1,AF=$\sqrt{2}$,则BD的长是$\sqrt{10}$.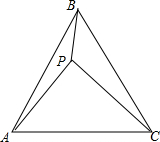 如图,△ABC是等边三角形,P是△ABC内一点,且满足PA2+PB2=PC2.
如图,△ABC是等边三角形,P是△ABC内一点,且满足PA2+PB2=PC2.