题目内容
如图,已知AM∥BN,AC平分∠MAB,BC平分∠NBA.
(1)过点C作直线DE,分别交AM、BN于点D、E,则AB、AD、BE三条线的长度之间存在何种等量关系?请直接写出关系式 .
(2)如图,若将直线DE绕点C转动,使DE与AM交于点D,与NB的延长线交于点E,则AB、AD、BE三条线的长度之间存在何种等量关系?请你给出结论并加以证明.

(1)过点C作直线DE,分别交AM、BN于点D、E,则AB、AD、BE三条线的长度之间存在何种等量关系?请直接写出关系式
(2)如图,若将直线DE绕点C转动,使DE与AM交于点D,与NB的延长线交于点E,则AB、AD、BE三条线的长度之间存在何种等量关系?请你给出结论并加以证明.

考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:探究型
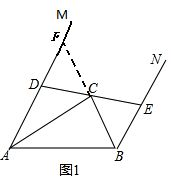
分析:(1)延长BC与AM交于点F,如图1,由AM∥BN,BC平分∠NBA可推出∠AFB=∠ABF,则有AF=AB.由AC平分∠MAB可得FC=BC,从而可证到△DCF≌△ECB,则有DF=EB,从而可得到AB=AF=AD+DF=AD+BE;
(2)延长BC与AM交于点F,如图2,可借鉴(1)中的解题经验得到AF=AB,DF=EB,从而得到AB=AF=AD-DF=AD-BE.
(2)延长BC与AM交于点F,如图2,可借鉴(1)中的解题经验得到AF=AB,DF=EB,从而得到AB=AF=AD-DF=AD-BE.
解答:解:(1)AB=AD+BE.
理由如下:延长BC与AM交于点F,如图1.
 ∵AM∥BN,BC平分∠NBA,
∵AM∥BN,BC平分∠NBA,
∴∠AFB=∠FBE,∠FBE=∠ABF,
∴∠AFB=∠ABF,
∴AF=AB.
∵AC平分∠MAB,
∴FC=BC.
在△DCF和△ECB中,
,
∴△DCF≌△ECB,
∴DF=EB,
∴AB=AF=AD+DF=AD+BE,
故答案为AB=AD+BE;
(2)AB=AD-BE.
证明:延长BC与AM交于点F,如图2.
∵AM∥BN,BC平分∠NBA,
∴∠AFB=∠FBN,∠FBN=∠ABF,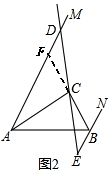
∴∠AFB=∠ABF,
∴AF=AB.
∵AC平分∠MAB,
∴FC=BC.
在△DCF和△ECB中,
,
∴△DCF≌△ECB,
∴DF=EB,
∴AB=AF=AD-DF=AD-BE.
理由如下:延长BC与AM交于点F,如图1.
 ∵AM∥BN,BC平分∠NBA,
∵AM∥BN,BC平分∠NBA,∴∠AFB=∠FBE,∠FBE=∠ABF,
∴∠AFB=∠ABF,
∴AF=AB.
∵AC平分∠MAB,
∴FC=BC.
在△DCF和△ECB中,
|
∴△DCF≌△ECB,
∴DF=EB,
∴AB=AF=AD+DF=AD+BE,
故答案为AB=AD+BE;
(2)AB=AD-BE.
证明:延长BC与AM交于点F,如图2.
∵AM∥BN,BC平分∠NBA,
∴∠AFB=∠FBN,∠FBN=∠ABF,

∴∠AFB=∠ABF,
∴AF=AB.
∵AC平分∠MAB,
∴FC=BC.
在△DCF和△ECB中,
|
∴△DCF≌△ECB,
∴DF=EB,
∴AB=AF=AD-DF=AD-BE.
点评:本题主要考查了全等三角形的判定与性质、角平分线的定义、等腰三角形的判定与性质等知识,由本题可得到以下经验:平行线与角平分线组合常常会出现等腰三角形;平行线与中点组合常常会出现全等三角形.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 如图所示,两个天平都平衡,则三个球体的重量等于( )个正方体的重量.
如图所示,两个天平都平衡,则三个球体的重量等于( )个正方体的重量.| A、2 | B、3 | C、4 | D、5 |
 如图,已知圆0的半径为10mm,弦AB=16mm,则圆心O到AB的距离是( )
如图,已知圆0的半径为10mm,弦AB=16mm,则圆心O到AB的距离是( )| A、3mm | B、4mm |
| C、6mm | D、8mm |
展览馆有A,B两个入口,D、E、F三个出口,则从A入口进,F出口出的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
△ABC中,三边长分别为a、b、c,已知:a=4,b=9,则下列命题正确的是( )
| A、c可以是最小边 | ||
| B、c是最大边 | ||
C、c可以等于3
| ||
| D、a不一定是最小边 |
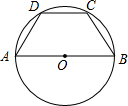 如图,四边形ABCD是⊙O的内接四边形,其中AB是⊙O的直径,已知AD=CD,CD∥AB,则∠BCD的度数是
如图,四边形ABCD是⊙O的内接四边形,其中AB是⊙O的直径,已知AD=CD,CD∥AB,则∠BCD的度数是 如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE
如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE 如图,它是一个正方体的展开图,若此正方体的相对面上的数互为相反数,则a-(b-c)=
如图,它是一个正方体的展开图,若此正方体的相对面上的数互为相反数,则a-(b-c)=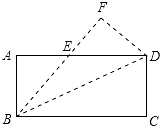 如图,矩形ABCD中,BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E.
如图,矩形ABCD中,BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E.