题目内容
13. 已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,且AO=CO.求证:四边形ABCD是平行四边形.
已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,且AO=CO.求证:四边形ABCD是平行四边形.
分析 由AB∥CD,AO=CO,利用ASA,可判定△AOB≌△COD,则可证得AB=CD,然后由一组对边平行且相等的四边形是平行四边形,证得四边形ABCD是平行四边形.
解答 证明:∵AB∥CD,
∴∠BAO=∠DCO,
在△AOB和△COD中,
$\left\{\begin{array}{l}{∠BAO=∠DCO}\\{AO=CO}\\{∠AOB=∠COD}\end{array}\right.$,
∴△AOB≌△COD(ASA),
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形.
点评 此题考查了平行四边形的判定以及全等三角形的判定与性质.注意证得△AOB≌△COD是关键.

练习册系列答案
相关题目
1.为备战中考,同学们积极投入复习,卓玛同学的试卷袋里装有语文试卷2张,臧文试卷3张,英语试卷1张,从中任意抽出一张试卷,恰好是语文试卷的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
18.已知am=5,an=6,则am+n的值为( )
| A. | 11 | B. | 30 | C. | $\frac{5}{6}$ | D. | $\frac{6}{5}$ |
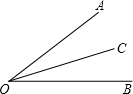 若射线OC是∠AOB的平分线.
若射线OC是∠AOB的平分线. 如图,已知a∥b,∠1=55°,则∠2=125°.
如图,已知a∥b,∠1=55°,则∠2=125°.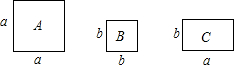 如图,正方形卡片A类、B类和长方形卡片C类各有若干张,如果要拼一个长为(a+2b),宽为(a+b)的大长方形,求需要A、B、C类卡片各多少张?并请用这些卡片拼出符合条件的长方形(画出示意图,并标明卡片类型即可)
如图,正方形卡片A类、B类和长方形卡片C类各有若干张,如果要拼一个长为(a+2b),宽为(a+b)的大长方形,求需要A、B、C类卡片各多少张?并请用这些卡片拼出符合条件的长方形(画出示意图,并标明卡片类型即可) 半径为2的图中扇形AOB的圆心角为150°,请你在圆内画出这个扇形,并求它的面积.
半径为2的图中扇形AOB的圆心角为150°,请你在圆内画出这个扇形,并求它的面积.