题目内容
20.解方程组$\left\{\begin{array}{l}{x+y+z=4}\\{4x+2y-z=-1}\\{x-y+2z=5}\end{array}\right.$.分析 对于方程组$\left\{\begin{array}{l}{x+y+z=4①}\\{4x+2y-z=-1②}\\{x-y+2z=5③}\end{array}\right.$,先利用①+②得5x+3y=3④,再利用①×2-③得x+3y=3⑤,则用④-⑤可求出x,然后利用代入法可分别求出y和z的值,从而得到方程组的解.
解答 解:$\left\{\begin{array}{l}{x+y+z=4①}\\{4x+2y-z=-1②}\\{x-y+2z=5③}\end{array}\right.$,
①+②得5x+3y=3④,
①×2-③得x+3y=3⑤,
④-⑤得4x=0,
解得x=0,
把x=0代入⑤得3y=3,
解得y=1,
把x=0,y=1代入①得0+1+z=4,
解得z=3.
所以方程组的解为$\left\{\begin{array}{l}{x=0}\\{y=1}\\{z=3}\end{array}\right.$.
点评 本题考查了解三元一次方程组:利用代入消元法和加减消元法把解三元一次方程组的问题转化为解二元一次方程组的问题.

练习册系列答案
相关题目
10.若|2a|=-2a,则a一定是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
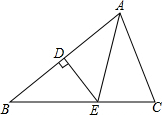 已知,如图,∠ABC中,AB=BC,DE是AB的中垂线,且BE=AC,求证:∠B=∠EAC.
已知,如图,∠ABC中,AB=BC,DE是AB的中垂线,且BE=AC,求证:∠B=∠EAC.