题目内容
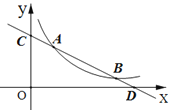
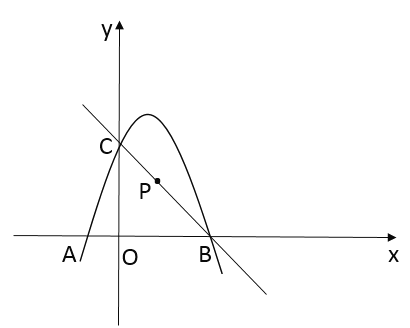
【题目】如图，在平面直角坐标系中，二次函数
的图像经过点
，点
，与
轴交于点
，
（1）求
、
的值：
（2）若点
为直线
上一点，点到直线
、
两点的距离相等，将该抛物线向左(或向右）平移，得到一条新抛物线，并且新抛物线经过点，求新抛物线的顶点坐标.
【答案】（1）
，
；（2）平移后函数的顶点为
或
【解析】
(1)将点A(-1,0)和点B(3,0)代入得到a，b的方程组，求出方程组的解得到a，b的值；
(2)先求出P点的坐标，令
得
，
，可知函数需向左平移
个单位或向右平移个单位，即可求得新抛物线的顶点坐标.
(1)∵抛物线
的图像经过点
，点
，
∴
，
解这个方程组得：
，
∴，
(2）∵点
到直线
、
两点的距离相等，
∴点P在抛物线的对称轴上，
设直线
的解析式为y=kx+b,经过，C(0,3),
∴y=-x+3,
又∵点为直线上一点，
令得，
由此可知，函数需向左平移个单位或向右平移个单位
原函数顶点为
∴平移后函数的顶点为或
练习册系列答案
相关题目
【题目】某水果经销商上月份销售一种新上市的水果，平均售价为10元/千克，月销售量为1000千克.经市场调查，若将该种水果价格调低至x元/千克，则本月份销售量y（千克）与x（元/千克）之间符合一次函数关系，并且得到了表中的数据：
价格x（元/千克） | 7 | 5 |
价格y（千克） | 2000 | 4000 |
（1）求y与x之间的函数解析式；
（2）已知该种水果上月份的成本价为5元/千克，本月份的成本价为4元/千克，要使本月份销售该种水果所获利润比上月份增加20％，同时又要让顾客得到实惠，那么该种水果价格每千克应调低至多少元?
