题目内容
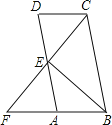
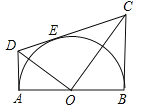
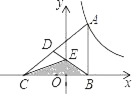
【题目】如图,在同一平面内,将两个全等的等腰直角![]() 和
和![]() 摆放在一起,
摆放在一起,![]() 为公共顶点,
为公共顶点,![]() ,它们的斜边长为2,若
,它们的斜边长为2,若![]() 固定不动,
固定不动,![]() 绕点
绕点![]() 旋转,
旋转,![]() 、
、![]() 与边
与边![]() 的交点分别为
的交点分别为![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合,点
重合,点![]() 不与点
不与点![]() 重合),设
重合),设![]() ,
,![]() .
.

(1)请在图中找出两对相似而不全等的三角形,并选取其中一对加以证明.
(2)求![]() 与
与![]() 的函数关系式,直接写出自变量
的函数关系式,直接写出自变量![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;证明见解析;(2)
;证明见解析;(2)![]() ,或
,或![]() .
.
【解析】
(1)根据“两角对应相等的两个三角形相似”,可知△ABE∽△DAE,△DCA∽△DAE;
(2)由(1)知,![]() ,
,![]() ,则有
,则有![]() ,因为相似三角形的对应边成比例,所以
,因为相似三角形的对应边成比例,所以![]() ,再把已知数据代入求解即可.
,再把已知数据代入求解即可.
解:(1)![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]()
又![]()
∴![]() .
.
(2)由(1)可知![]() ,
,![]() ,则有
,则有![]() .
.
∴![]()
又∵![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,
,
∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,或
,或![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目