Question

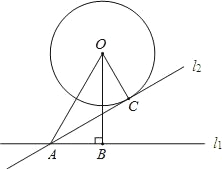
【题目】如图，⊙O与直线l1相离，圆心O到直线l1的距离OB＝2，OA＝4，将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C，则OC＝_____．

Answer 1

【答案】2．

【解析】

在直角△ABO中，利用正弦三角函数的定义求得∠OAB=60°，然后由旋转的角度、图中角与角间的和差关系知∠OAC=30°；最后由切线的性质推知△AOC是直角三角形，在直角三角形中由“30°角所对的直角边是斜边的一半”即可求得OC．

解：∵OB⊥AB，OB=2，OA=4，
∴在直角△ABO中，sin∠OAB=＝，则∠OAB=60°；
又∵∠CAB=30°，
∴∠OAC=∠OAB-∠CAB=30°；
∵直线l2刚好与⊙O相切于点C，
∴∠ACO=90°，
∴在直角△AOC中，OC=OA=2（30°角所对的直角边是斜边的一半）．
故答案是：2．