Question

【题目】如图，抛物线与x轴交于点A（，0）、点B（2，0），与y轴交于点C（0，1），连接BC．

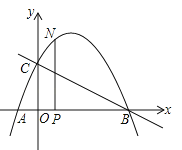
（1）求抛物线的函数关系式；

（2）点N为抛物线上的一个动点，过点N作NP⊥x轴于点P，设点N的横坐标为t（），求△ABN的面积S与t的函数关系式；

（3）若且时△OPN∽△COB，求点N的坐标．

Answer 1

【答案】（1）；（2）；（3）（， ）或（1，2）．

【解析】试题（1）可设抛物线的解析式为，用待定系数法就可得到结论；

（2）当时，点N在x轴的上方，则NP等于点N的纵坐标，只需求出AB，就可得到S与t的函数关系式；

（3）由相似三角形的性质可得PN=2PO．而PO=，需分和0＜t＜2两种情况讨论，由PN=2PO得到关于t的方程，解这个方程，就可得到答案．

试题解析：（1）设抛物线的解析式为，把C（0，1）代入可得： ，∴，∴抛物线的函数关系式为： ，即；

（2）当时， ＞0，∴NP===，

∴S=ABPN==；

（3）∵△OPN∽△COB，∴，∴，∴PN=2PO．

①当时，PN===，PO== ，∴，整理得：，解得： =， =，∵＞0， ＜＜0，∴t=，此时点N的坐标为（， ）；

②当0＜t＜2时，PN===，PO==t，∴，整理得： ，解得： =， =1．∵＜0，0＜1＜2，∴t=1，此时点N的坐标为（1，2）．

综上所述：点N的坐标为（， ）或（1，2）．