题目内容
解方程:x2-3|x|-4=0.
考点:解一元二次方程-因式分解法,绝对值
专题:分类讨论,整体思想,因式分解
分析:讨论x的范围去绝对值,得到关于x的一元二次方程,利用因式分解法求解;也可看作为|x|的一元二次方程,利用因式分解法求解.
解答:解:方法1
显然x≠0.当x>0时,x2-3x-4=0,
所以x1=4,x2=-1(舍去).
当x<0时,x2+3x-4=0,
所以x3=-4,x4=1(舍去).
所以原方程的根为x1=4,x2=-4.
方法2
由于x2=|x|2,所以|x|2-3|x|-4=0,
所以(|x|-4)(|x|+1)=0,
所以|x|=4,|x|=-1(舍去).
所以x1=4,x2=-4.
显然x≠0.当x>0时,x2-3x-4=0,
所以x1=4,x2=-1(舍去).
当x<0时,x2+3x-4=0,
所以x3=-4,x4=1(舍去).
所以原方程的根为x1=4,x2=-4.
方法2
由于x2=|x|2,所以|x|2-3|x|-4=0,
所以(|x|-4)(|x|+1)=0,
所以|x|=4,|x|=-1(舍去).
所以x1=4,x2=-4.
点评:本题考查了利用因式分解法把一元二次方程转化为两个一元一次方程求解的能力.要熟练掌握因式分解的方法.同时考查了绝对值的意义和整体思想的运用.

练习册系列答案
相关题目
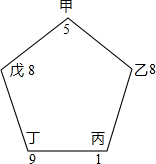 甲、乙、丙、丁、戊五名同学手拉手围成一个五边形,每个人心中想一个数,相邻的两个人把所想两数的平均数告诉与他们不相邻的那个人,结果如图所示,则乙心中所想的数是
甲、乙、丙、丁、戊五名同学手拉手围成一个五边形,每个人心中想一个数,相邻的两个人把所想两数的平均数告诉与他们不相邻的那个人,结果如图所示,则乙心中所想的数是 在△ABC中,AH⊥BC于H,D,E,F分别是BC,CA,AB的中点(如图所示).求证:∠DEF=∠HFE.
在△ABC中,AH⊥BC于H,D,E,F分别是BC,CA,AB的中点(如图所示).求证:∠DEF=∠HFE.