题目内容
13.已知一组数为:1,$\frac{3}{4}$,$\frac{5}{9}$,$\frac{7}{16}$…按此规律,用代数式表示第n个数为$\frac{2n-1}{{n}^{2}}$.分析 分子是从1开始连续的奇数,分母是从1开始连续自然数的平方,由此规律得出第n个数为$\frac{2n-1}{{n}^{2}}$.
解答 解:∵一组数为:1,$\frac{3}{4}$,$\frac{5}{9}$,$\frac{7}{16}$…,
∴第n个数为$\frac{2n-1}{{n}^{2}}$.
故答案为:$\frac{2n-1}{{n}^{2}}$.
点评 此题考查数字的变化规律,找出分子分母之间的联系,得出数字之间的运算规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列说法错误的是( )
| A. | 绝对值等于本身的数只有1 | B. | a的相反数是-a | ||
| C. | 立方后等于本身的数是-1,0,1 | D. | 任何数与0相乘,都得0 |
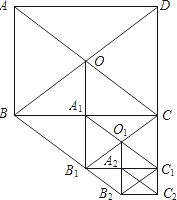 如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则S${\;}_{平行四边形OB{B}_{1}C}$=6,S${\;}_{平行四边形{O}_{1}{B}_{1}{B}_{2}{C}_{1}}$=$\frac{3}{2}$.
如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则S${\;}_{平行四边形OB{B}_{1}C}$=6,S${\;}_{平行四边形{O}_{1}{B}_{1}{B}_{2}{C}_{1}}$=$\frac{3}{2}$.