题目内容
4.在平面直角坐标系中,已知一次函数y=kx+b的图象过点P(1,1),与x轴交于点A,与y轴交于点B,且tan∠OBP=$\frac{1}{2}$,那么点A的坐标是($\frac{1}{2}$,0)或($\frac{3}{2}$,0).分析 根据tan∠OBP=$\frac{1}{2}$,判断出一次函数斜率,求出函数解析式即可求出A点坐标.
解答  解:如图,
解:如图,
∵tan∠OBP=$\frac{1}{2}$,
∴k=2或-2,
故解析式为①y=2x+b或②y=-2x+b,
把P(1,1)分别代入①、②得,b=-1或b=3,
一次函数解析式为①y=2x-1,②y=-2x+3.
与x轴交点为A($\frac{1}{2}$,0)或($\frac{3}{2}$,0).
点评 本题考查了一次函数图象上点的坐标特征,根据所给正切值求出斜率是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
13.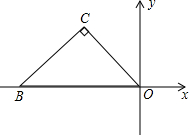 如图,在直角坐标系中,△OBC的顶点O(0,0),B(-4,0),且∠0CB=90°,OC=BC,则点C关于y轴对称的点的坐标是( )
如图,在直角坐标系中,△OBC的顶点O(0,0),B(-4,0),且∠0CB=90°,OC=BC,则点C关于y轴对称的点的坐标是( )
 如图,在直角坐标系中,△OBC的顶点O(0,0),B(-4,0),且∠0CB=90°,OC=BC,则点C关于y轴对称的点的坐标是( )
如图,在直角坐标系中,△OBC的顶点O(0,0),B(-4,0),且∠0CB=90°,OC=BC,则点C关于y轴对称的点的坐标是( )| A. | (2,3) | B. | (2,2) | C. | (-2,-2) | D. | (2$\sqrt{2}$,2$\sqrt{2}$) |
15.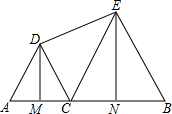 如图,AB=2a,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着点A向点B的方向移动(不与点A、B重合),连接DE,得到四边形DMNE.这个四边形的面积为( )
如图,AB=2a,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着点A向点B的方向移动(不与点A、B重合),连接DE,得到四边形DMNE.这个四边形的面积为( )
 如图,AB=2a,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着点A向点B的方向移动(不与点A、B重合),连接DE,得到四边形DMNE.这个四边形的面积为( )
如图,AB=2a,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着点A向点B的方向移动(不与点A、B重合),连接DE,得到四边形DMNE.这个四边形的面积为( )| A. | a2 | B. | $\frac{\sqrt{3}}{2}$a2 | C. | $\frac{\sqrt{3}}{4}$a2 | D. | 不能确定 |
9.一个饲养场里的鸡的只数与猪的头数之和是70,鸡、猪的腿数之和是196,设鸡的只数是x,依题意列方程为( )
| A. | 2x+4(70-x)=196 | B. | 2x+4×70=196 | C. | 4x+2(70-x)=196 | D. | 4x+2×70=196 |
13.使函数y=$\sqrt{4-2x}$有意义的自变量x的取值范围是( )
| A. | x≤2 | B. | x≠2 | C. | x≥2 | D. | x<2 |
14.下列代数运算正确的是( )
| A. | (x2)3=x5 | B. | (2x)3=2x3 | C. | x•x3=x4 | D. | (x-1)2=x2-1 |
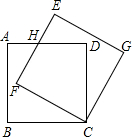 如图所示,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,
如图所示,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,