Question

正方形ABCD的边长为acm，E、F分别是BC、CD的中点，连接BF、DE，则图中阴影部分的面积是

 

 cm²．

Answer 1

考点：正方形的性质

专题：几何图形问题

分析：连接BD，可看出阴影部分的面积等于

1

2

正方形的面积+一个三角形的面积，用相似求出三角形的面积，阴影部分的面积可证．

解答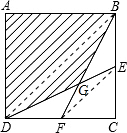：解：连接BD，EF．
∵阴影部分的面积=△ABD的面积+△BDG的面积 （G为BF与DE的交点），
∴△ABD的面积=

1

2

正方形ABCD的面积=

1

2

a²．
∵△BCD中EF为中位线，
∴EF∥BD，EF=

1

2

BD，
∴△GEF∽△GBD，
∴DG=2GE，
∴△BDE的面积=

1

2

△BCD的面积．
∴△BDG的面积=

2

3

△BDE的面积=

1

3

△BCD的面积=

1

3

•

1

2

a²=

1

6

a²．
∴阴影部分的面积=

1

2

a²+

1

6

a²=

2

3

a²．
故答案为：

2

3

a²．

点评：本题考查正方形的性质，正方形的四个边长相等，关键是连接BD，把阴影部分分成两部分计算．