题目内容
9.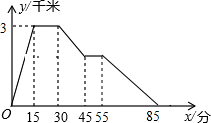 张强从家跑步去体育场,在那里锻炼了一阵后又到文具店买笔,然后散步回家.已知张强家、体育场、文具店在同一直线上,他从家跑步到体育场的平均速度是他从体育场到文具店的平均速度的2倍.设他出发后所用的时间为x(单位:min),离家的距离为y(单位:km),y与x的函数关系如图所示,则下列说法中错误的是( )
张强从家跑步去体育场,在那里锻炼了一阵后又到文具店买笔,然后散步回家.已知张强家、体育场、文具店在同一直线上,他从家跑步到体育场的平均速度是他从体育场到文具店的平均速度的2倍.设他出发后所用的时间为x(单位:min),离家的距离为y(单位:km),y与x的函数关系如图所示,则下列说法中错误的是( )| A. | 体育场离张强家的距离为3km | |
| B. | 体育场离文具店的距离为1.5km | |
| C. | 张强从体育场到文具店的平均速度为100m/min | |
| D. | 张强从文具店散步回家的平均速度为60m/min |
分析 因为张强从家直接到体育场,故第一段函数图象所对应的y轴的最高点即为体育场离张强家的距离,即可判断A;求出从家跑步到体育场的平均速度,除以2是他从体育场到文具店的平均速度,即可判断C;再乘以从体育场到文具店的时间,即可判断B;先求出张强家离文具店的距离,再求出从文具店到家的时间,求出二者的比值即可.
解答 解:由函数图象可知,体育场离张强家的距离为3千米,故A选项正确;
∵张强15分钟从家跑步去体育场,
∴从家跑步到体育场的平均速度为:3÷15=0.2(千米/分),
∴从体育场到文具店的平均速度为:0.2÷2=0.1(千米/分)=100(米/分),故C选项正确;
∵从体育场到文具店的时间为:45-30=15(分),
∴体育场离文具店的距离为0.1×15=1.5(千米),故B选项正确;
∵文具店离张强家3-1.5=1.5千米,张强从文具店散步走回家花了85-55=30分,
∴张强从文具店回家的平均速度是:1.5÷30=0.05(千米/分)=50(米/分),故D选项错误.
故选D.
点评 本题主要考查一次函数的应用,速度=路程÷时间的应用,正确理解函数图象横纵坐标表示的意义是解答此题的关键.

练习册系列答案
相关题目
18.下列计算结果正确的是( )
| A. | 2+$\sqrt{3}$=2$\sqrt{3}$ | B. | $\sqrt{8}÷\sqrt{2}$=2 | C. | (-2a2)3=-6a6 | D. | (a+1)2=a2+1 |
17.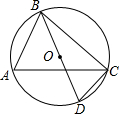 如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )
如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )
 如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )
如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
14.某网上电器商城销售某种品牌的高端电器.已知该电器按批发价上浮50%进行标价,若按照标价的九折销售,则可获纯利润350元,现由于商城搞促销,该电器按照标价的八折销售,则可获纯利润( )
| A. | 180元 | B. | 200元 | C. | 220元 | D. | 240元 |
1.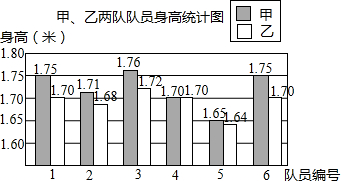 某校要成立一支由6名女生组成的舞蹈队,初三(1)、(2)班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如图,部分统计量如表:(单位:米)
某校要成立一支由6名女生组成的舞蹈队,初三(1)、(2)班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如图,部分统计量如表:(单位:米)
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的概率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队中哪个队被录取?请说明理由.
 某校要成立一支由6名女生组成的舞蹈队,初三(1)、(2)班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如图,部分统计量如表:(单位:米)
某校要成立一支由6名女生组成的舞蹈队,初三(1)、(2)班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如图,部分统计量如表:(单位:米) | 平均数 | 标准差 | 中位数 | |
| 甲队 | 1.72 | 0.038 | 1.73 |
| 乙队 | 1.69 | 0.025 | 1.70 |
(2)求乙队身高的平均数及身高不小于1.70米的概率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队中哪个队被录取?请说明理由.
18.下列计算不正确的是( )
| A. | x2•x3=x5 | B. | (x3)2=x6 | C. | x3+x3=x6 | D. | ($\sqrt{3}$x)2=3x2 |
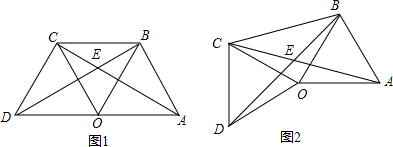
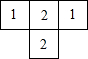 由6个小立方体组成的几何体的俯视图如图1所示,每个小正方形上的数字表示该位置上摆放的小立方体的个数,则该几何体的左视图应为( )
由6个小立方体组成的几何体的俯视图如图1所示,每个小正方形上的数字表示该位置上摆放的小立方体的个数,则该几何体的左视图应为( )