题目内容
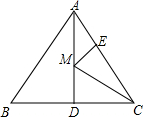 如图,等边△ABC的边长为12,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=4,EM+CM的最小值为
如图,等边△ABC的边长为12,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=4,EM+CM的最小值为考点:轴对称-最短路线问题,等边三角形的性质
专题:
分析:要求EM+CM的最小值,需考虑通过作辅助线转化EM,CM的值,从而找出其最小值求解.
解答:解:连接BE,与AD交于点M.则BE就是EM+CM的最小值.
取CE中点F,连接DF.
∵等边△ABC的边长为12,AE=4,
∴CE=AC-AE=12-4=8,
∴CF=EF=AE=4,
又∵AD是BC边上的中线,
∴DF是△BCE的中位线,
∴BE=2DF,BE∥DF,
又∵E为AF的中点,
∴M为AD的中点,
∴ME是△ADF的中位线,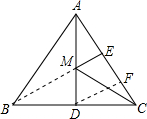
∴DF=2ME,
∴BE=2DF=4ME,
∴BM=BE-ME=4ME-ME=3ME,
∴BE=
BM.
在直角△BDM中,BD=
BC=6,DM=
AD=3
,
∴BM=
=3
,
∴BE=4
.
∵EM+CM=BE,
∴EM+CM的最小值为4
.
故答案为:4
.
取CE中点F,连接DF.
∵等边△ABC的边长为12,AE=4,
∴CE=AC-AE=12-4=8,
∴CF=EF=AE=4,
又∵AD是BC边上的中线,
∴DF是△BCE的中位线,
∴BE=2DF,BE∥DF,
又∵E为AF的中点,
∴M为AD的中点,
∴ME是△ADF的中位线,

∴DF=2ME,
∴BE=2DF=4ME,
∴BM=BE-ME=4ME-ME=3ME,
∴BE=
| 4 |
| 3 |
在直角△BDM中,BD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴BM=
| BD2+DM2 |
| 7 |
∴BE=4
| 7 |
∵EM+CM=BE,
∴EM+CM的最小值为4
| 7 |
故答案为:4
| 7 |
点评:此题主要考查了等边三角形的性质和轴对称及勾股定理等知识的综合应用.得出M点位置是解题关键.

练习册系列答案
相关题目
在一个不透明的盒子里有形状、大小相同的黄球2个、红球3个,从盒子里任意摸出1个球,摸到红球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
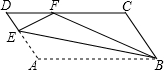 如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为8,△FCB的周长为32,则FC的长为
如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为8,△FCB的周长为32,则FC的长为 如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是
如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是