Question

【题目】如图，已知在中，，点是的中点，连结并延长，与的延长线相交于点，连结．若，，则四边形的面积是_________．

Answer 1

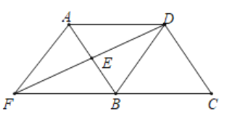
【答案】20

【解析】

由ASA证明△ADE≌△BFE，得出BF=AD，DE=FE，证出四边形AFBD是菱形，在Rt△BDE中，由三角函数得出DE=2BE，设BE=x，则DE=2x，由勾股定理得出方程，解方程求出，得出AB=2BE=2，DF=2DE=4BE=4，再由菱形面积公式即可得出结果．

∵四边形ABCD是平行四边形，
∴AD=BC=5，AB∥CD，AD∥BC，
∴∠BDC=∠DBE，∠ADE=∠BFE，
∵BD=BC=5，
∴AD=BD=5，
∵点E是AB的中点，
∴DE⊥AB，AE=BE，
∴AF=BF，
在△ADE和△BFE中，

，
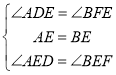∴△ADE≌△BFE（ASA），
∴BF=AD，DE=FE，
∴AD=BD=BF=AF，
∴四边形AFBD是菱形，
在Rt△BDE中，tan∠DBE=tan∠BDC=2，

∴，

∴DE=2BE，
设BE=，则DE=，
由勾股定理得：+=，即+=，
解得：，

∴AB=2BE=2，DF=2DE=4BE=4，

∴四边形AFBD的面积=；
故答案为：．