题目内容
如图，∠AOB=60°，O1，O2，O3…是∠AOB平分线上的点，其中OO1=2，若O1，O2，O3…分别以为圆心作圆，使得⊙O1，⊙O2，⊙O3…均与∠AOB的两边相切，且相邻两圆相外切，则⊙O2014的面积是 （结果保留π）
解：设⊙O1，⊙O2，⊙O3…与OB的切点分别为C，D，E，
连接CO1，DO2，EO3，
∴CO1⊥BO，DO2⊥BO，EO3⊥BO，
∵∠AOB=60°，O1，O2，O3…是∠AOB平分线上的点，其中OO1=2，
∴∠O1OC=30°，
∴CO1=1
，
∴DO2=
（2+1+DO2），
∴DO2=3，
同理可得出：EO3=9，
∴⊙O2014的半径为：32013，
∴⊙O2014的面积是π×（32013）2=34026π．
故答案为：34026π．
练习册系列答案
相关题目
，BD＝
，则AB的长为 ( )
如图，当半径分别是5和r的两圆⊙O1和⊙O2外切时，它们的圆心距O1O2=8，则⊙O2的半径r为（ ）
|
| A． | 12 | B． | 8 | C． | 5 | D． | 3 |
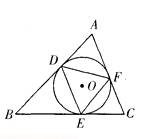如图，已知△ABC的内切圆⊙O与各边相切于点D、E、F，则点O是△DEF的 ( ) 
三
条中线的交点
剪去
圆周的一个扇形，将留下的扇形围成一个圆锥(接缝处不重叠)，那么这个圆锥的高为 ( )
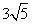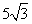cm
cm