题目内容
若2(
+
+
)=x+y+z,求x+y-z的值.
| x |
| y-1 |
| z-2 |
考点:配方法的应用,非负数的性质:偶次方
专题:计算题
分析:已知等式变形,利用非负数的性质求出x,y,z的值,即可确定出x+y-z的值.
解答:解:已知等式变形得:x-2
+1+y-1-2
+1-(z-2+2
+1)=0,
即(
-1)2+(
-1)2+(
)2=0,
∴
=1,
=1,
=0,
解得:x=1,y=2,z=2,
则x+y-z=1+2-2=1.
| x |
| y-1 |
| z-2 |
即(
| x |
| y-1 |
| z-2 |
∴
| x |
| y-1 |
| z-2 |
解得:x=1,y=2,z=2,
则x+y-z=1+2-2=1.
点评:此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
若关于x的方程
-1=0有增根,求a的值( )
| ax+1 |
| x-1 |
| A、0 | B、-1 | C、1 | D、-2 |
 如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.
如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.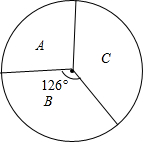 某校对1500名在校学生进行每周上网的情况调查,A为每天上网的学生,B为从不上网的学生,C为偶尔上网的学生,如扇形统计图所示,根据注释,解答以下问题:
某校对1500名在校学生进行每周上网的情况调查,A为每天上网的学生,B为从不上网的学生,C为偶尔上网的学生,如扇形统计图所示,根据注释,解答以下问题: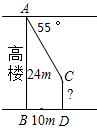 如图,王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为55°,又知水平距离BD=10m,楼高AB=24m,则树高CD等于
如图,王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为55°,又知水平距离BD=10m,楼高AB=24m,则树高CD等于