题目内容
 如图,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是
如图,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是
- A.72°
- B.63°
- C.54°
- D.36°
B
分析:连接BE,根据CD切⊙O于B,由弦切角定理知,∠CBE=∠A,利用直径所对的角是直角可得∠AEB=90°-∠A=∠EBC+∠C=∠A+36°,从而求得∠ABD=∠AEB=90°-27°=63°.
解答: 解:连接BE,
解:连接BE,
∵CD切⊙O于B,
∴∠CBE=∠A,
∵∠AEB=90°-∠A=∠EBC+∠C=∠A+36°,
∴∠A=27°,
∴∠ABD=∠AEB=90°-27°=63°.
故选B.
点评:本题利用了弦切角定理,直径对的圆周角是直角,三角形的外角与内角的关系即可求解.
分析:连接BE,根据CD切⊙O于B,由弦切角定理知,∠CBE=∠A,利用直径所对的角是直角可得∠AEB=90°-∠A=∠EBC+∠C=∠A+36°,从而求得∠ABD=∠AEB=90°-27°=63°.
解答:
 解:连接BE,
解:连接BE,∵CD切⊙O于B,
∴∠CBE=∠A,
∵∠AEB=90°-∠A=∠EBC+∠C=∠A+36°,
∴∠A=27°,
∴∠ABD=∠AEB=90°-27°=63°.
故选B.
点评:本题利用了弦切角定理,直径对的圆周角是直角,三角形的外角与内角的关系即可求解.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 8、如图,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是( )
8、如图,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是( ) 如图,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是
如图,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是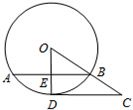 10,sin∠COD=
10,sin∠COD=
 如图,CD切⊙O于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为15,sin∠COD=
如图,CD切⊙O于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为15,sin∠COD=