题目内容
如图，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，则∠ABD的度数是分析：连接OB，由切线的性质知△OBC是直角三角形，可求出∠COB的度数．由于∠COB是等腰△AOB的外角，由此可求出∠OBA的度数，已知∠OBA和∠ABD互余，即可得解．
解答：
解：连接OB，则∠OBC=90°；
Rt△COB中，∠C=36°，
∴∠COB=90°-∠C=54°；
∵OA=OB，
∴∠OBA=∠OAB=
∠COB=27°，
∴∠ABD=90°-∠OBA=63°．
解：连接OB，则∠OBC=90°；Rt△COB中，∠C=36°，
∴∠COB=90°-∠C=54°；
∵OA=OB，
∴∠OBA=∠OAB=
| 1 |
| 2 |
∴∠ABD=90°-∠OBA=63°．
点评：本题考查的知识点有：切线的性质、等腰三角形的性质、三角形外角和内角的关系等知识．
练习册系列答案
阅读快车系列答案
相关题目
8、如图，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，则∠ABD的度数是（ ）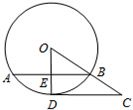
10，sin∠COD=
如图，CD切⊙O于点D，连结OC，交⊙O于点B，过点B作弦AB⊥OD，点E为垂足，已知⊙O的半径为15，sin∠COD=