题目内容
18. 填写推理理由
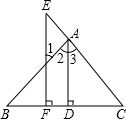
填写推理理由如图,已知AD⊥BC于D,EF⊥BC于F,AD平分∠BAC.说明∠E=∠1的理由.
解:∵AD⊥BC,EF⊥BC( 已知 )
∴∠ADC=∠EFC=90°( 垂直的意义 )
∴AD∥EF (同位角相等,两直线平行)
∴∠1=∠2(两直线平行,内错角相等)
∠E=∠CAD(两直线平行,内错角相等)
又∵AD平分∠BAC( 已知 )
∴∠BAD=∠CAD
∴∠1=∠E.
分析 求出AD∥EF,根据平行线的性质得出∠1=∠2,∠E=∠CAD,推出∠2=∠CAD,根据角平分线定义得出即可.
解答 解:∵AD⊥BC,EF⊥BC( 已知 ),
∴∠ADC=∠EFC=90°( 垂直的意义 ),
∴AD∥EF (同位角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等),
∠E=∠3(两直线平行,同位角相等),
又∵AD平分∠BAC( 已知 )
∴∠BAD=∠CAD,
∴∠1=∠E,
故答案为:同位角相等,两直线平行,∠2,两直线平行,内错角相等,∠CAD,两直线平行,同位角相等,∠CAD.
点评 本题考查了垂直定义,平行线的性质和判定,角平分线定义的应用,能求出∠BAD=∠CAD是解此题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
8.六边形ABCDEF∽六边形A′B′C′D′E′F′,AB:A′B′=2:3,下列说法中不正确的是( )
| A. | ∠C=∠C′ | |
| B. | 3DE=2D′E′ | |
| C. | S六边形ABCDEF:S六边形A′B′C′D′E′F′=4:9 | |
| D. | 两个六边形的周长相等 |
7.-2的相反数是( )
| A. | .-2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | -$\frac{4}{5}$ |

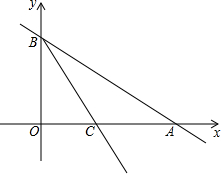 如图,已知A、B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,如果OA,OB的长分别是x2-14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,
如图,已知A、B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,如果OA,OB的长分别是x2-14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,