��Ŀ����
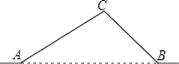
����Ŀ����֪����ͼ1��ֱ��y= ![]() x+6��x�ᡢy��ֱ��ڵ�A��C���㣬��B�ĺ�����Ϊ2��
x+6��x�ᡢy��ֱ��ڵ�A��C���㣬��B�ĺ�����Ϊ2�� 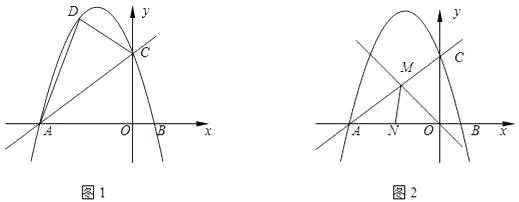
��1����A��C���������������ߵĺ�����ϵʽ��
��2����D��ֱ��AC�Ϸ�������������һ�㣬PΪ�߶�AC��һ�㣬��S��PCD=2S��PAD �� ���P�����ꣻ
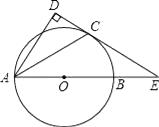
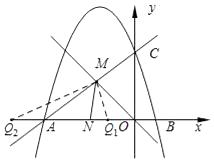
��3����ͼ2������һ��ֱ��y=��x��ֱ��AC���ڵ�M��NΪ�߶�OA��һ�㣬��AMN=��AOM����QΪx�Ḻ������һ�㣬�ҵ�Q��ֱ��MN��ֱ��MO�ľ�����ȣ����Q�����꣮
���𰸡�
��1���⣺��y= ![]() x+6�У�
x+6�У�
��x=0����y=6����y=0����x=��8��
��A����8��0����C��0��6����
�ߵ�B�ĺ�����Ϊ2��
��B��2��0����
�������߽���ʽΪy=a��x+8����x��2������
��C��0��6�����룬��6=a������16����
��a=�� ![]() ��
��
��y=�� ![]() ��x+8����x��2����
��x+8����x��2����
�� ![]()
��2���⣺��ͼ��ʾ����P��PH��AO��H��
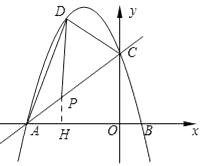
��S��PCD=2S��PAD��
��AP��PC=1��2��
��PH��CO��
��AH��HO=1��2��
��OH= ![]() AO��
AO��
�֡�AO=8��
��OH=8�� ![]() =
= ![]() ��
��
���P�ĺ�����Ϊ ![]() ��
��
��ֱ��y= ![]() x+6�У���x=
x+6�У���x= ![]() ʱ��y=
ʱ��y= ![]() ����
���� ![]() ��+6=2��
��+6=2��
���P��������Ϊ2��
���P�������� ![]() ��2��
��2��
��3���⣺�����������
�ٵ���Q1Ϊ��NMO��ƽ������x��Ľ���ʱ����Q1��ֱ��MN��ֱ��MO�ľ�����ȣ�
��ֱ��y=��x��ֱ��y= ![]() x+6���ڵ�M��
x+6���ڵ�M��
��M���� ![]() ��
�� ![]() ����
����
�֡�A����8��0����
�����������빫ʽ�ɵ�AM= ![]() =
= ![]() ��
��
�ߡ�AMN=��AOM����MAN=��OAM��
���AMN�ס�AOM��
��AM2=AN��AO������ ![]() ��2=AN��8��
��2=AN��8��
��AN= ![]() ��
��
��ON=AO��AN= ![]() ��
��
��N���� ![]() ��0����
��0����
�����������빫ʽ�ɵ�MN= ![]() ��MO=
��MO= ![]() ��
��
��MQ1ƽ�֡�NMO��
�� ![]() =
= ![]() =
= ![]() ��
��
��OQ1= ![]() NO=
NO= ![]() =
= ![]() ��
��
����Q1�������� ![]() ��0����
��0����
�ڵ���Q2Ϊ��NMO���ڲ��ǵ�ƽ������x��Ľ���ʱ����Q2��ֱ��MN��ֱ��MO�ľ�����ȣ�
����Q1�� ![]() ��0����M����
��0����M���� ![]() ��
�� ![]() �����ɵ�
�����ɵ�
ֱ��MQ1����ʽΪy=��3x�� ![]() ��
��
��MQ1��MQ2��
�����ֱ��MQ2����ʽΪy= ![]() x+b��
x+b��
��M���� ![]() ��
�� ![]() �����룬�ɵ�b=
�����룬�ɵ�b= ![]() ��
��
��ֱ��MQ2����ʽΪy= ![]() x+
x+ ![]() ��
��
�൱y=0ʱ��0= ![]() x+
x+ ![]() ��
��
���x=�� ![]() ��
��
����Q2�������� ![]() ��0����
��0����
������������Q�������� ![]() ��0����
��0���� ![]() ��0��
��0��
����������1������ֱ��y= ![]() x+6���ɵ�A����8��0����C��0��6�����������߽���ʽΪy=a��x+8����x��2������C��0��6�����룬�ɵ������ߵĺ�����ϵʽ����2����P��PH��AO��H������S��PCD=2S��PAD �� �ɵ�AP��PC=1��2����AH��HO=1��2�������õ�OH=
x+6���ɵ�A����8��0����C��0��6�����������߽���ʽΪy=a��x+8����x��2������C��0��6�����룬�ɵ������ߵĺ�����ϵʽ����2����P��PH��AO��H������S��PCD=2S��PAD �� �ɵ�AP��PC=1��2����AH��HO=1��2�������õ�OH= ![]() AO=8��
AO=8�� ![]() =
= ![]() ����ֱ��y=
����ֱ��y= ![]() x+6�У���x=
x+6�У���x= ![]() ʱ��y=
ʱ��y= ![]() ����
���� ![]() ��+6=2���ɵõ�P������Ϊ��
��+6=2���ɵõ�P������Ϊ�� ![]() ��2������3������������������ۣ��ٵ���Q1Ϊ��NMO��ƽ������x��Ľ���ʱ����Q1��ֱ��MN��ֱ��MO�ľ�����ȣ��ڵ���Q2Ϊ��NMO���ڲ��ǵ�ƽ������x��Ľ���ʱ����Q2��ֱ��MN��ֱ��MO�ľ�����ȣ��������������ε��������N����
��2������3������������������ۣ��ٵ���Q1Ϊ��NMO��ƽ������x��Ľ���ʱ����Q1��ֱ��MN��ֱ��MO�ľ�����ȣ��ڵ���Q2Ϊ��NMO���ڲ��ǵ�ƽ������x��Ľ���ʱ����Q2��ֱ��MN��ֱ��MO�ľ�����ȣ��������������ε��������N���� ![]() ��0�����ٸ��ݽ�ƽ���ߵ����ʿɵõ�Q1������Ϊ��
��0�����ٸ��ݽ�ƽ���ߵ����ʿɵõ�Q1������Ϊ�� ![]() ��0����������MQ1��MQ2 �� �ɵ�ֱ��MQ2����ʽΪy=
��0����������MQ1��MQ2 �� �ɵ�ֱ��MQ2����ʽΪy= ![]() x+
x+ ![]() �������õ���Q2������Ϊ��
�������õ���Q2������Ϊ�� ![]() ��0����
��0����
�����㾫����ͨ��������ý�ƽ���ߵ����ʶ��������������ε��ж������ʣ���������1���ڽǵ�ƽ�����ϵĵ㵽����ǵ����ߵľ�����ȣ� ����2��һ���ǵ����ߵľ�����ȵĵ㣬������ǵ�ƽ�����ϣ����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ�������Խ����⣮

 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�