Question

【题目】在平面直角坐标系xOy中，已知第一象限内的点A在反比例函数y＝的图象上，第二象限内的点B在反比例函数y＝的图象上，连接OA、OB，若OA⊥OB，OB＝OA，则k＝_____．

Answer 1

【答案】-2

【解析】

过点A作AD⊥x轴于点D，过点B作BC⊥x轴于点C，点A的坐标为（a，），证明△OCB≌△ADO，便可用a表示点B的坐标，再把B点坐标代入反比例函数y＝中求得k．

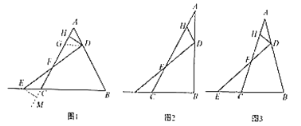
解：过点A作AD⊥x轴于点D，过点B作BC⊥x轴于点C，

则有∠ADO＝∠OCB＝90°．

设点A的坐标为（a，），

∴OD＝a，AD＝

∵OA⊥OB，

∴∠AOB＝90°，

∴∠DOA＝90°﹣∠COB＝∠CBO，

在△OCB和△ADO中，∠OCB=∠ADO，∠CBO=∠DOA，OB=AO，

∴△OCB≌△ADO（AAS），

∴BC＝OD＝a，OC＝AD＝

∴B（﹣），

∴k=

故答案为﹣2．