ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЎ
ЃЎ
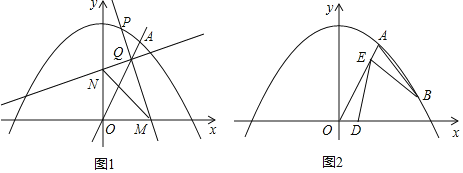
![]() ЧѓжБЯп
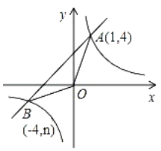
ЧѓжБЯп![]() ЕФНтЮіЪНКЭЯпЖЮOAЕФГЄЖШЃЛ
ЕФНтЮіЪНКЭЯпЖЮOAЕФГЄЖШЃЛ
![]() ЕуPЮЊХзЮяЯпЕквЛЯѓЯоФкЕФЖЏЕуЃЌЙ§ЕуPзїжБЯпPMЃЌНЛxжсе§АыжсгкЕу
ЕуPЮЊХзЮяЯпЕквЛЯѓЯоФкЕФЖЏЕуЃЌЙ§ЕуPзїжБЯпPMЃЌНЛxжсе§АыжсгкЕу![]() ЕуMЁЂOВЛжиКЯ
ЕуMЁЂOВЛжиКЯ![]() ЃЌНЛжБЯпOAгкЕуQЃЌдйЙ§ЕуQзїжБЯпPMЕФДЙЯпЃЌНЛyжсе§АыжсгкЕуNЃЌСЌНсMNЃЌШє
ЃЌНЛжБЯпOAгкЕуQЃЌдйЙ§ЕуQзїжБЯпPMЕФДЙЯпЃЌНЛyжсе§АыжсгкЕуNЃЌСЌНсMNЃЌШє![]() ЃЌЪдЧѓ
ЃЌЪдЧѓ![]() МАЕуQЕФзјБъЃЛ
МАЕуQЕФзјБъЃЛ
![]() ШчЭМ2ЃЌШєЕуBЮЊХзЮяЯпЩЯЖдГЦжсгвВрЕФЕуЃЌЕуEдкЯпЖЮOAЩЯ
ШчЭМ2ЃЌШєЕуBЮЊХзЮяЯпЩЯЖдГЦжсгвВрЕФЕуЃЌЕуEдкЯпЖЮOAЩЯ![]() гыЕуOЁЂAВЛжиКЯ
гыЕуOЁЂAВЛжиКЯ![]() ЃЌЕу
ЃЌЕу![]() ЪЧxжсе§АыжсЩЯЕФЖЏЕуЃЌЧвТњзу
ЪЧxжсе§АыжсЩЯЕФЖЏЕуЃЌЧвТњзу![]() МЬајЬНОПЃКmШЁКЮжЕЪБЃЌЗћКЯЬѕМўЕФEЕуЕФИіЪ§жЛга1ИіЃЎ
МЬајЬНОПЃКmШЁКЮжЕЪБЃЌЗћКЯЬѕМўЕФEЕуЕФИіЪ§жЛга1ИіЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ2,
ЃЈ2ЃЉ2,![]() ЃЈ3ЃЉЕБ
ЃЈ3ЃЉЕБ![]() ЪБЃЌEЕужЛга1Иі
ЪБЃЌEЕужЛга1Иі
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉШчЭМ1жаЃЌЙ§ЕуQзї![]() жсгкЕуGЃЌ
жсгкЕуGЃЌ![]() жсгкЕу
жсгкЕу![]() Щш
Щш![]() ЕБQHгыQMжиКЯЪБЃЌЯдШЛQGгыQNжиКЯЃЌДЫЪБ
ЕБQHгыQMжиКЯЪБЃЌЯдШЛQGгыQNжиКЯЃЌДЫЪБ![]() ЃЛ
ЃЛ![]() ЕБQHгыQMВЛжиКЯЪБЃЌгЩ
ЕБQHгыQMВЛжиКЯЪБЃЌгЩ![]() Ёз
Ёз![]() ЃЌМДПЩНтОіЮЪЬтЃЛ
ЃЌМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉШчД№ЭМ2жаЃЌбгГЄABНЛxжсгкЕуFЃЌЙ§ЕуFзї![]() гкЕуCЃЌЙ§ЕуAзї
гкЕуCЃЌЙ§ЕуAзї![]() жсгкЕу
жсгкЕу![]() ЪзЯШЧѓГіЕуFзјБъЃЌABЕФГЄЃЌдйжЄУї
ЪзЯШЧѓГіЕуFзјБъЃЌABЕФГЄЃЌдйжЄУї![]() Ёз
Ёз![]() ЃЌЩш
ЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌгЩ
ЃЌгЩ![]() Ёз
Ёз![]() ЕУ
ЕУ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌЭЦГі
ЃЌЭЦГі![]() ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтМДПЩЃЛ
ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтМДПЩЃЛ
НтЃК![]() АбЕу
АбЕу![]() ДњШы
ДњШы![]() ЕУЃЛ
ЕУЃЛ
![]()
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
![]() ШчЭМ1жаЃЌЙ§ЕуQзї
ШчЭМ1жаЃЌЙ§ЕуQзї![]() жсгкЕуGЃЌ
жсгкЕуGЃЌ![]() жсгкЕу
жсгкЕу![]() Щш
Щш![]()
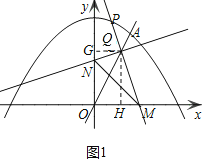
![]() ЕБQHгыQMжиКЯЪБЃЌЯдШЛQGгыQNжиКЯЃЌДЫЪБ
ЕБQHгыQMжиКЯЪБЃЌЯдШЛQGгыQNжиКЯЃЌДЫЪБ![]() ЃЛ
ЃЛ
![]() ЕБQHгыQMВЛжиКЯЪБЃЌ
ЕБQHгыQMВЛжиКЯЪБЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
гж![]()
![]() Ёз
Ёз![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() span>ЃЌ
span>ЃЌ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
![]()
![]() ШчД№ЭМ2жаЃЌбгГЄABНЛxжсгкЕуFЃЌЙ§ЕуFзї
ШчД№ЭМ2жаЃЌбгГЄABНЛxжсгкЕуFЃЌЙ§ЕуFзї![]() гкЕуCЃЌЙ§ЕуAзї
гкЕуCЃЌЙ§ЕуAзї![]() жсгкЕуRЃЎ
жсгкЕуRЃЎ
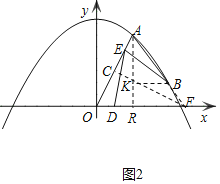
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() Ёз
Ёз![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() ЃЌ
ЃЌ
ЩшЕу![]() ЃЌ
ЃЌ
Й§ЕуBзї![]() гкЕуKЃЌдђ
гкЕуKЃЌдђ![]() Ёз
Ёз![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
МД ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЩсШЅ
ЩсШЅ![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЧѓABвВПЩВЩгУЯТУцЕФЗНЗЈ
ЧѓABвВПЩВЩгУЯТУцЕФЗНЗЈ![]()
ЩшжБЯпAFЮЊ![]() АбЕу
АбЕу![]() ЃЌЕу
ЃЌЕу![]() ДњШыЕУ
ДњШыЕУ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
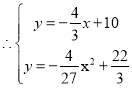 ЃЌ
ЃЌ
![]() ЩсШЅ
ЩсШЅ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
дк![]() гы
гы![]() жа
жа
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() Ёз
Ёз![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
гЩ![]() Ёз
Ёз![]() ЕУ
ЕУ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЖЅЕуЮЊ
ЖЅЕуЮЊ![]()
ШчД№ЭМ3ЃЌ

ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌДЫЪБEЕуга1ИіЃЛ
ЃЌДЫЪБEЕуга1ИіЃЛ
ЕБ![]() ЪБЃЌШЮШЁвЛИіmЕФжЕЖМЖдгІзХСНИіaжЕЃЌДЫЪБEЕуга2ИіЃЎ
ЪБЃЌШЮШЁвЛИіmЕФжЕЖМЖдгІзХСНИіaжЕЃЌДЫЪБEЕуга2ИіЃЎ
![]() ЕБ
ЕБ![]() ЪБЃЌEЕужЛга1ИіЃЎ
ЪБЃЌEЕужЛга1ИіЃЎ

 дФЖСПьГЕЯЕСаД№АИ
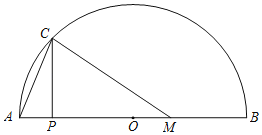
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПШчЭМЃЌдкАыдВЛЁABжаЃЌжБОЖABЃН6cmЃЌЕуMЪЧABЩЯвЛЕуЃЌMBЃН2cmЃЌPЮЊABЩЯвЛЖЏЕуЃЌPCЁЭABНЛABгкЕуCЃЌСЌНгACКЭCMЃЌЩшAЁЂPСНЕуМфЕФОрРыЮЊxcmЃЌAЁЂCСНЕуМфЕФОрРыЮЊy1cmЃЌCЁЂMСНЕуМфЕФОрРыЮЊy2cmЃЎ
аЁЖЋИљОнбЇЯАКЏЪ§ЕФОбщЃЌЗжБ№ЖдКЏЪ§y1ЁЂy2ЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃК
ЯТУцЪЧаЁЖЋЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉАДееЯТБэжаздБфСПxЕФжЕНјааШЁЕуЁЂЛЭМЁЂВтСПЃЌЗжБ№ЕУЕНСЫy1ЃЌy2гыxЕФМИзщЖдгІжЕЃЛ
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.45 | 3.46 | 4.90 | 5.48 | 6 | |
y2/cm | 4 | 3.74 | 3.46 | 3.16 | 2.83 | 2.45 | 2 |
ЃЈ2ЃЉдкЭЌвЛЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіВЙШЋКѓЕФБэжаИїзщЪ§жЕЫљЖдгІЕФЕуЃЈxЃЌy1ЃЉЃЌЃЈxЃЌy2ЃЉЃЌВЂЛГіКЏЪ§y1ЃЌy2ЕФЭМЯѓЃЛ

ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃК
ЂйЕБACЃОCMЪБЃЌЯпЖЮAPЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЛ
ЂкЕБЁїAMCЪЧЕШбќШ§НЧаЮЪБЃЌЯпЖЮAPЕФГЄдМЮЊЁЁ ЁЁЃЎ