题目内容
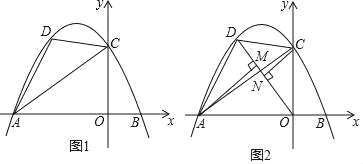
【题目】已知,如图1,直线y=![]() x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为
x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为![]() ,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
(1)求抛物线的函数关系式;
(2)若P为线段AC上一点,且S△PCD=2S△PAD,求点P的坐标;
(3)如图2,连接OD,过点A、C分别作AM⊥OD,CN⊥OD,垂足分别为M、N.当AM+CN的值最大时,求点D的坐标.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+3;(2)点P的坐标为(﹣
x+3;(2)点P的坐标为(﹣![]() ,1);(3)当AM+CN的值最大时,点D的坐标为(
,1);(3)当AM+CN的值最大时,点D的坐标为(![]() ,
,![]() ).
).
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A、C的坐标,由点B所在的位置结合点B的横坐标可得出点B的坐标,根据点A、B、C的坐标,利用待定系数法即可求出抛物线的函数关系式;
(2)过点P作PE⊥x轴,垂足为点E,则△APE∽△ACO,由△PCD、△PAD有相同的高且S△PCD=2S△PAD,可得出CP=2AP,利用相似三角形的性质即可求出AE、PE的长度,进而可得出点P的坐标;
(3)连接AC交OD于点F,由点到直线垂线段最短可找出当AC⊥OD时AM+CN取最大值,过点D作DQ⊥x轴,垂足为点Q,则△DQO∽△AOC,根据相似三角形的性质可设点D的坐标为(﹣3t,4t),利用二次函数图象上点的坐标特征可得出关于t的一元二次方程,解之取其负值即可得出t值,再将其代入点D的坐标即可得出结论.
(1)∵直线y=![]() x+3与x轴、y轴分别交于A、C两点,
x+3与x轴、y轴分别交于A、C两点,
∴点A的坐标为(﹣4,0),点C的坐标为(0,3).
∵点B在x轴上,点B的横坐标为![]() ,
,
∴点B的坐标为(![]() ,0),
,0),
设抛物线的函数关系式为y=ax2+bx+c(a≠0),
将A(﹣4,0)、B(![]() ,0)、C(0,3)代入y=ax2+bx+c,得:
,0)、C(0,3)代入y=ax2+bx+c,得:
 ,解得:
,解得: ,
,
∴抛物线的函数关系式为y=﹣![]() x2﹣
x2﹣![]() x+3;
x+3;
(2)如图1,过点P作PE⊥x轴,垂足为点E,
∵△PCD、△PAD有相同的高,且S△PCD=2S△PAD,
∴CP=2AP,
∵PE⊥x轴,CO⊥x轴,
∴△APE∽△ACO,
∴![]() ,
,
∴AE=![]() AO=
AO=![]() ,PE=
,PE=![]() CO=1,
CO=1,
∴OE=OA﹣AE=![]() ,
,
∴点P的坐标为(﹣![]() ,1);
,1);
(3)如图2,连接AC交OD于点F,
∵AM⊥OD,CN⊥OD,
∴AF≥AM,CF≥CN,
∴当点M、N、F重合时,AM+CN取最大值,
过点D作DQ⊥x轴,垂足为点Q,则△DQO∽△AOC,
∴![]() ,
,
∴设点D的坐标为(﹣3t,4t).
∵点D在抛物线y=﹣![]() x2﹣
x2﹣![]() x+3上,
x+3上,
∴4t=﹣3t2+![]() t+3,
t+3,
解得:t1=﹣![]() (不合题意,舍去),t2=
(不合题意,舍去),t2=![]() ,
,
∴点D的坐标为(![]() ,
,![]() ),
),
故当AM+CN的值最大时,点D的坐标为(![]() ,
,![]() ).
).

【题目】勾股定理是数学中最常见的定理之一,熟练的掌握勾股数,对迅速判断、解答题目有很大帮助,观察下列几组勾股数:
|
|
| |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
| |
… | … | … | … |
|
|
|
|
(1)你能找出它们的规律吗?(填在上面的横线上)
(2)你能发现![]() ,
,![]() ,
,![]() 之间的关系吗?
之间的关系吗?
(3)对于偶数,这个关系 (填“成立”或“不成立”)吗?
(4)你能用以上结论解决下题吗?
![]()