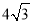��Ŀ����
�������龳��
��֪���ε����Ϊa��aΪ������a��0�������þ��εij�Ϊ����ʱ�������ܳ���С����Сֵ�Ƕ��٣�
����ѧģ�͡�
��þ��εij�Ϊx���ܳ�Ϊy����y��x�ĺ�������ʽΪy=2��x+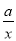 ����x��0����
����x��0����
��̽���о���
С������ǰ�о������ľ��飬��̽������y=x+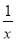 ��ͼ�����ʣ�
��ͼ�����ʣ�
��1����������龳������y=x+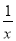 ���Ա���x��ȡֵ��Χ��x��0���±���y��x�ļ����Ӧֵ��
���Ա���x��ȡֵ��Χ��x��0���±���y��x�ļ����Ӧֵ��
x | �� |
|
|
| 1 | 2 | 3 | m | �� |
y | �� | 4 | 3 | 2 | 2 | 2 | 3 | 4 | �� |
��д��m��ֵ��
�ڻ����ú���ͼ���ͼ�ó���x=�� ��ʱ��y����Сֵ��y��С=�� ����
��ʾ��������κ���y=ax2+bx+c��a��0�������С��ֵʱ������ͨ���۲�ͼ������ͨ���䷽�õ��������䷽������y=x+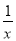 ��x��0������Сֵ��������⣨2��
��x��0������Сֵ��������⣨2��
��������⡿
��2��ֱ��д���������龳��������Ľ��ۣ�
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
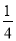
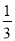
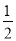
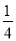
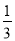
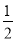
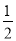
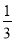
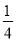

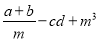 =________.
=________. B.
B.  C.
C.  D.
D. 
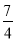 B. k����
B. k����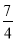 ��k��0
��k��0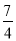 D. k�ݩ�
D. k�ݩ�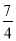 ��k��0
��k��0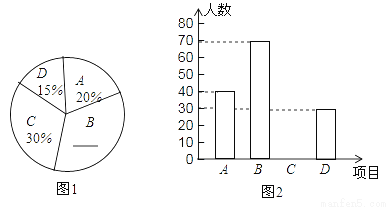
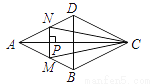
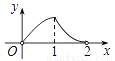 B.
B. 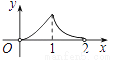
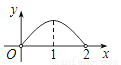 D.
D. 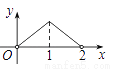
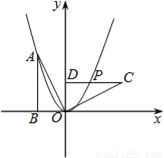
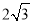 B.
B. 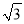 C.
C. 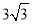 D.
D.