Question

【题目】在平面直角坐标系中，点A的坐标为(-3,3)，以A为顶点的∠BAC的两边始终与x轴交于B、C两点（B在C左面），且∠BAC=45°.过点A作AD⊥x轴，垂足为D，当DC=1时，将∠BAC沿AC所在直线翻折，翻折后边AB交y轴于点M，则点M的坐标是_____．

Answer 1

【答案】（0,1.5）或（0，-3）

【解析】

当点C在点D右侧时，连接CM，过点A作AE⊥y轴于点E，证明△BAD≌△MAE，在Rt△COM中，由勾股定理即可求得M的坐标；当点C在点D左侧时，连接CM，过点A作AF⊥y轴于点F，证明△BAD≌△MAF，同理，在Rt△COM中，由勾股定理即可求得M的坐标．

解：设OM=x，

当点C在点D右侧时，如图2，连接CM，过点A作AE⊥y轴于点E，

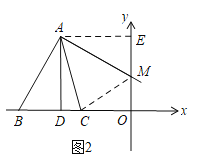
由∠BAM=∠DAE=90°，

可知：∠BAD=∠MAE；

∴在△BAD和△MAE中， ，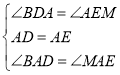

∴△BAD≌△MAE．

∴BD=EM=3-x．

又∵AC=AC，∠BAC=∠MAC，

∴△BAC≌△MAC．

∴BC=CM=4-x．
在Rt△COM中，由勾股定理得：
OC2+OM2=CM2，即22+x2=（4-x）2，
解得：x=1.5，

∴M点坐标为（0，1.5）．

当点C在点D左侧时，如图3，连接CM，过点A作AF⊥y轴于点F，

同理，△BAD≌△MAF，

∴BD=FM=3+x．

同理，△BAC≌△MAC，

∴BC=CM=2+x．

在Rt△COM中，由勾股定理得：

OC2+OM2=CM2，即42+x2=（2+x）2，

解得：x=3，

∴M点坐标为（0，-3）．
综上，M的坐标为（0，1.5）或（0，-3）．