题目内容
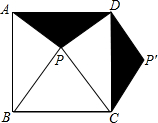正方形ABCD内一点P，使△PBC为等边三角形，连接PA，PD，把△PAD绕点D以逆时针方向旋转90°得△DCP?，则∠DCP?=________度．
15
分析：△PBC为等边三角形，则CP=CD，AB=BP，由旋转的性质可得△CPD，△BPA是等腰三角形，进而可得∠PCD=∠ABP=30°，由三角形内角和定理可求得，∠BAP与∠DCP?的大小．
解答：△PBC为等边三角形，则CP=CD，AB=BP，
故△CPD，△BPA是等腰三角形，
∠PCD=∠ABP=30°，
由三角形内角和定理可求得∠BAP=75°，∠DCP?=∠DCP=15°．
故答案为15°．
点评：本题利用了正方形和等边三角形的性质，三角形内角和定理，等腰三角形的性质求解．
分析：△PBC为等边三角形，则CP=CD，AB=BP，由旋转的性质可得△CPD，△BPA是等腰三角形，进而可得∠PCD=∠ABP=30°，由三角形内角和定理可求得，∠BAP与∠DCP?的大小．
解答：△PBC为等边三角形，则CP=CD，AB=BP，
故△CPD，△BPA是等腰三角形，
∠PCD=∠ABP=30°，
由三角形内角和定理可求得∠BAP=75°，∠DCP?=∠DCP=15°．
故答案为15°．
点评：本题利用了正方形和等边三角形的性质，三角形内角和定理，等腰三角形的性质求解．
练习册系列答案
阅读快车系列答案
相关题目
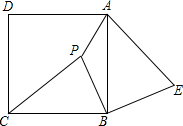已知：如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE=∠CBP，BE=BP．
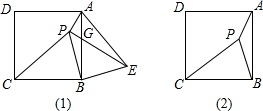如图（1），P是正方形ABCD内一点，将△PBC绕点B按顺时针方向旋转后与△EBA重合．
如图，P是正方形ABCD内一点，将△ABP绕B顺时针旋转90°到△CBP′位置，若BP=a，则PP′=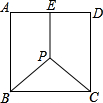
如图，正方形ABCD内一点P，PE⊥AD于E，若PB=PC=PE=5，则正方形的边长为