题目内容
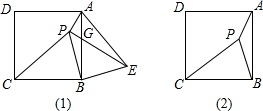 如图(1),P是正方形ABCD内一点,将△PBC绕点B按顺时针方向旋转后与△EBA重合.
如图(1),P是正方形ABCD内一点,将△PBC绕点B按顺时针方向旋转后与△EBA重合.(1)若PB=a,求PE的长;
(2)如图(2),P是正方形ABCD内一点,设PA=a,PB=
| 2 |
分析:(1)根据旋转图形得出对应线段之间的等量关系,再得出旋转角的度数,进而求出结果;
(2)根据已知△PBC绕点B按顺时针方向旋转后与△EBA重合,得出PB=BE=
a,以及∠APE=90°,利用勾股定理求出即可.
(2)根据已知△PBC绕点B按顺时针方向旋转后与△EBA重合,得出PB=BE=
| 2 |
解答:解:(1)∵△PBC绕点B按顺时针方向旋转后与△EBA重合,
∴AB与BC重合,BP=BE=a,
∴△PBC绕点B按顺时针方向旋转了90°后与△EBA重合,
∴∠PBE=90°,
∴PE=
=
a
(2)∵△PBC绕点B按顺时针方向旋转后与△EBA重合,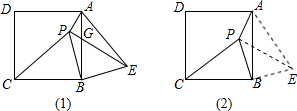
∴PB=BE=
a,∠PBE=90°,
∴PE=2a,
∵AE=PC,
∵PA=a,∠APB=135°,
∴∠APE=90°,
则PC=AE=
a.
∴AB与BC重合,BP=BE=a,
∴△PBC绕点B按顺时针方向旋转了90°后与△EBA重合,
∴∠PBE=90°,
∴PE=
| BE2+PB2 |
| 2 |
(2)∵△PBC绕点B按顺时针方向旋转后与△EBA重合,

∴PB=BE=
| 2 |
∴PE=2a,
∵AE=PC,
∵PA=a,∠APB=135°,
∴∠APE=90°,
则PC=AE=
| 5 |
点评:此题主要考查了旋转图形的性质,以及勾股定理与等腰三角形的性质等知识,根据旋转得出对应线段之间的等量关系,是解决问题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
