题目内容

精英家教网如图，P是正方形ABCD内一点，将△ABP绕B顺时针旋转90°到△CBP′位置，若BP=a，则PP′=
 
．
分析：由△ABP绕B顺时针旋转90°得到△CBP′，根据旋转的性质得到∠PBP′=90°，BP=BP′=a，即△BPP′为等腰直角三角形，利用勾股定理即可得到PP′．
解答：解：∵△ABP绕B顺时针旋转90°得到△CBP′，
∴∠PBP′=90°，BP=BP′=a，
即△BPP′为等腰直角三角形，
∴PP′=
2
BP=
2
a．
故答案为：
2
a．
点评：本题考查了旋转的性质，旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．同时考查了正方形的性质和等腰直角三角形的性质．
练习册系列答案
相关题目
精英家教网如图，E是正方形ABCD对角线AC上一点，EF⊥AB，EG⊥BC，F、G是垂足，若正方形ABCD周长为a，则EF+EG等于（　　）
A、
1
4
a
B、
1
2
a
C、a
D、2a
如图①，已知△ABC中，AB=AC，点P是BC上的一点，PN⊥AC于点N，PM⊥AB于点M，CG⊥AB于点G点．
（1）则CG、PM、PN三者之间的数量关系是
 
；
（2）如图②，若点P在BC的延长线上，则PM、PN、CG三者是否还有上述关系，若有，请说明理由，若没有，猜想三者之间又有怎样的关系，并证明你的猜想；
（3）如图③，AC是正方形ABCD的对角线，AE=AB，点P是BE上任一点，PN⊥AB于点N，PM⊥AC于点M，猜想PM、PN、AC有什么关系；（直接写出结论）
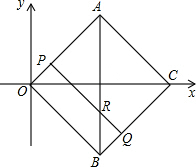精英家教网
22、如图，ABCD是正方形，P是对角线BD上一点，过P点作直线EF、GH分别平行于AB、BC，交两组对边于E、F、G、H，则四边形PEDG，四边形PHBF都是正方形，四边形PEAH、四边形PGCF都是矩形，设正方形PEDG的边长是a，正方形PHBF的边长是b． 请动手实践并得出结论：
（1）请你动手测量一些线段的长后，计算正方形PEDG与正方形PHBF的面积之和以及矩形PEAH与矩形PGCF的面积之和．
（2）你能根据（1）的结果判断a2+b2与2ab的大小吗？
（3）当点P在什么位置时，有a2+b2=2ab？
如图四边形AOBC是正方形，点C的坐标是（4
2
，0），动点P、Q同时从点O出发，点P沿着折线OACB的方向运动；点Q沿着折线OBCA的方向运动，设运动时间为t．
（1）求出经过O、A、C三点的抛物线的解析式．
（2）若点Q的运动速度是点P的2倍，点Q运动到边BC上，连接PQ交AB于点R，当AR=3
2
时，请求出直线PQ的解析式．
（3）若点P的运动速度为每秒1个单位长度，点Q的运动速度为每秒2个单位长度精英家教网，两点运动到相遇停止．设△OPQ的面积为S．请求出S关于t的函数关系式以及自变量t的取值范围．
（4）判断在（3）的条件下，当t为何值时，△OPQ的面积最大？
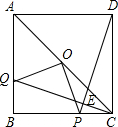如图，AC是正方形ABCD的对角线，点O是AC的中点，点Q是AB上一点，连接CQ，DP⊥CQ于点E，交BC于精英家教网点P，连接OP，OQ；
求证：
（1）△BCQ≌△CDP；
（2）OP=OQ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网